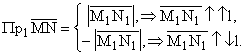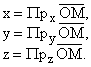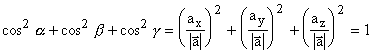Глава 15. Понятие вектора. Линейные операции над векторами. Координаты вектора

Величины, характеризующиеся только числовым значением (масса, объем, плотность, стоимость и другие), называются Скалярными.

Величины, характеризующиеся и числовым значением, и направлением (сила, скорость, момент силы и другие), называются Векторными.

Определение

Вектор – это Направленный отрезок, на котором определены операции сравнения сложения и умножения на вещественное число. Векторы обозначаются так: A, , , . 
(Рис. 2.1.1)

Рис. 2.1.1	Рис. 2.1.2–а	Рис. 2.1.2–б

Определение

Модуль (Длина) вектора обозначается так: |A|, b, .

Определение

Векторы, лежащие на одной или на параллельных прямых, называются Коллинеарными.

Определение

Векторы Равны тогда и только тогда, когда они:

1. коллинеарны;

2. одинаково направлены;

3. имеют равные длины.

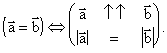
Вектор можно произвольно переносить параллельно самому себе, помещая его начало в любую точку пространства.

Вектор, длина которого равна нулю, называется Нулевым. Нулевой вектор не имеет определенного направления.

Определение

Векторы, лежащие в одной или в параллельных плоскостях, называются Компланарными. (Рис. 2.1.2–а и 2.1.2–б).

Линейные операции над векторами

1. Сложение векторов.

Определение

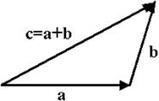
Суммой двух векторов A и B называется вектор C = a + b, начало которого совпадает с началом вектора A, а конец – с концом вектора B при условии, что начало вектора B совпадает с концом вектора A (рис. 3–а). Это правило сложения векторов называется еще “Правилом треугольника”.

Рис. 2.1.3–а	Рис. 2.1.3–б

Вектор C = a + b можно построить также по “Правилу параллелограмма”: в точке O совместим начала векторов A И B и на этих векторах, как на сторонах, построим параллелограмм. Вектор, совпадающий с диагональю этого параллелограмма с началом в точке O, и является вектором C (рис. 2.1.3–а).

Сумма векторов обладает как Переместительным свойством (рис. 2.1.3–б):

A + B = B + A

(2.1.1)

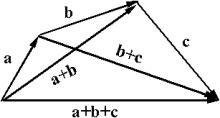
Так и Сочетательным (рис. 2.1.4):

(a + b) + c = a + (b + c).

(2.1.2)

Рис. 2.1.4

Подобно построению суммы трех векторов можно построить сумму любого конечного числа векторов.

2. Умножение вектора на число

Определение

Произведением вектора A на число L называется вектор C = LA, удовлетворяющий следующим условиям:

1. ;

2. A коллинеарен вектору A;

3. , если > 0 и , если < 0.

Определение

Вектор называется Противоположным вектору .

Можно убедиться, что произведение вектора на число обладает следующими свойствами:

(2.1.3)

Определение

Вектор, длина которого равна единице, называется Единичным.

Определение

Вектор , имеющий длину, равную единице и параллельный вектору , называется Ортом вектора .

Из определения умножения вектора на число следует, что , т. е. каждый вектор равен произведению его модуля на орт (единичный вектор того же направления).

3. Вычитание векторов.

Определение

Разностью Векторов A и B называется такой вектор C = A – B, сумма которого с вычитаемым вектором B дает вектор A (рис. 2.1.5–а).

.

(2.1.4)

Если на векторах A и B построить параллелограмм, то одна из диагоналей совпадает с суммой A + B, а другая – с разностью A – B (рис. 2.1.5–б).

Определение

Углом между векторами A И B называется наименьший угол , на который надо повернуть один из векторов до его совпадения со вторым (рис. 2.1.6).

Рис. 2.1.6

Проекция вектора на ось

Пусть даны в пространстве вектор и ось L. Точки M1 и N1 являются проекциями на ось L точек M и N (рис. 2.1.7).

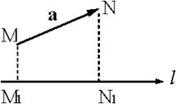
Рис. 2.1.7

Определение

Проекцией вектора на ось l называется число, равное длине вектора , лежащего на этой оси, если параллелен L, и длине вектора , взятой со знаком “минус”, если антипараллелен L.

(2.1.5)

Проекция вектора на ось обладает следующими свойствами:

, где – угол между и L, , .

(2.1.6)

Способы задания вектора

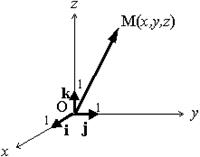
Пусть в пространстве задана прямоугольная система координат. Положение точки M (рис. 2.1.8) определяется с помощью координат x, y и z: M(x, y,z).

Рис. 2.1.8

(2.1.7)

Определение

Вектор называется Радиус–вектором точки M.

На каждой оси координат выберем единичный вектор, направленный также, как и ось. Обозначим эти векторы соответственно I, j, k. Совокупность этих векторов называется Базисом декартовой (прямоугольной) системы координат.

А) Задание вектора его координатами.

Определение

Координатами вектора A называются его проекции на координатные оси.

A = {ax, ay, az}

(2.1.8)

Где ax = , ay = , az = .

Из свойств проекций вектора на ось следует, что, если A = {ax, ay, az},

B = {bx, by, bz}, то A + B = {ax+bx, ay+by, az+bz}, A = { Ax, Ay, Az}, A – B = {ax–bx, ay–by, az–bz}.

(2.1.9)

Зная координаты вектора A, можно вычислить его длину по формуле

(2.1.10)

Векторы A = {ax, ay, az} и B = {bx, by, bz} коллинеарны тогда и только тогда, когда их координаты пропорциональны:

(2.1.11)

Б) Задание вектора его разложением по базису.

Рассмотрим вектор A = (рис. 2.1.9).

Рис. 2.1.9

Тогда

MI + nJ + pK.

(2.1.12)

Легко убедиться, что

M = ПрxA = ax, n = ПрyA = Ay, k = ПрzA = az.

(2.1.13)

Окончательно

A = axI + ayJ + azK.

(2.1.14)

Такое представление вектора называется его Разложением по базису I, J, K.

В) Задание вектора координатами его начала и конца.

Пусть , где M(x1,y1,z1), N(x2,y2,z2) (рис. 2.1.10).

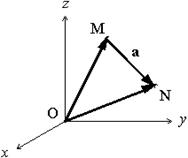
Рис. 2.1.10

Векторы и имеют такие же координаты, как и точки M и N соответственно:

={x1, y1, z1}, ={x2, y2, z2}.

(2.1.15)

Как следует из рис. 2.1.10, , тогда

A = {x2 x1, y2 y1, z2 z1}.

(2.1.16)

Следовательно

Ax = x2 x1, ay = y2 y1, az = z2 z1.

(2.1.17)

Расстояние между двумя точками определяется по формуле:

D = d(M, N) = .

Таким образом

D = .

(2.1.18)

Г) Задание вектора его модулем и направляющими косинусами.

Направляющими косинусами вектора называются углы, которые образует этот вектор с осями OX, OY и OZ. Они обозначаются , и (рис. 2.1.11).

Рис. 2.1.11

Если известны углы , , , а также модуль (длина) вектора A, то координаты вектора можно найти по формулам:

Ax = cos , ay = cos , az = cos .

(2.1.19)

Откуда

, , .

(2.1.20)

Определение

Cos , cos И cos Называются Направляющими косинусами вектора A.

Найдем сумму квадратов этих косинусов:

(2.1.21)

Формула cos2 + cos2 + cos2 = 1 выражает связь между направляющими косинусами.

Пример

Даны начало M(3,–2,4) и конец N(5,0,3) вектора A = . Найти координаты этого вектора и его длину.

Решение

Ax = xN – xM = 5–3=2; ay = yN – yM = 0–(–2)=2; az = zN – zM = 3–4=–1. Итак, вектор A = {2,2,–1}. Вычислим длину вектора A:

< Предыдущая		Следующая >