Глава 14. Евклидово пространство
Выше мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем Метрику, т. е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие Скалярного произведения.
Определение
Скалярным произведением двух векторов X=![]() и Y=
и Y=![]() Называется число
Называется число
|
|
(1.16.1) |
Скалярное произведение имеет Следующие свойства:
1. ![]() – коммутативное свойство.
– коммутативное свойство.
2. ![]() – дистрибутивное свойство.
– дистрибутивное свойство.
3. ![]() –для любого действительного числа α.
–для любого действительного числа α.
4. ![]() , если X ненулевой вектор,
, если X ненулевой вектор, ![]() , если X нулевой вектор.
, если X нулевой вектор.
Определение
Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется Евклидовым пространством.
Длиной (нормой) вектора X в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
|
|
(1.16.2) |
Имеют следующие свойства длины вектора:
1. ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
2. ![]() , где λ – действительное число.
, где λ – действительное число.
3. ![]() – неравенство Коши–Буняковского.
– неравенство Коши–Буняковского.
4. ![]() – неравенство треугольника.
– неравенство треугольника.
Угол φ между двумя векторами X и У определяется равенством
|
|
(1.16.3) |
Где ![]() .
.
Определение
Два вектора называются ортогональными, если их скалярное произведение равно нулю.
Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, если два ненулевых вектора ортогональны, то угол между ними равен ![]() .
.
Векторы E1 , e2 , … , en n–мерного евклидова пространства образуют ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т. е. (Ei ,ej) = 0 при ![]() и
и ![]() при
при ![]() .
.
Теорема
Во всяком N–мерном евклидовом пространстве существует ортонормированный базис.
14.1. Упражнения
1. Вычислить определители

2. Решить системы:
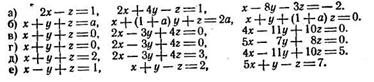
![]()
3. Вычислить площадь треугольника с вершинами в точках (1, –2), (2, 3), (4, 5).
4. Лежат ли три точки (1, 1), (3, 3), (0, 0) на одной прямой?
5. Составить уравнение прямой, проходящей через две точки (3, 2) и ( –1, 3).
6. Найти высоту треугольника с вершинами А(x1, y1), В(x2, y2), С(X3, y3).
7. ПОльзуясь решением предыдущего упражнения, найти площадь треугольника с вершинами А(x1, y1), В(x2, y2), С(X3, y3)
8. Показать, что площадь выпуклого четырехугольника ABCD С вершинами А(x1, y1), В(x2, y2), С(X3, y3), В(X4, y4) Равна
![]()
9. Вычислить определитель

10. Найти Х Из уравнений:

11. При каком порядке обхода вершин выражение в скобках будет иметь знак + ?
12. Упростить выражения:
![]()
13. Доказать тождество

| < Предыдущая | Следующая > |
|---|