Глава 13. n–мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, в которых определены операции сложения и умножения на число, являются простейшими примерами векторных пространств. Здесь мы приведем обобщение этих понятий на N–мерный случай.
Определение
Любой упорядоченный набор из N действительных чисел ![]() называется N–мерным вектором
называется N–мерным вектором ![]() ; при этом числа, составляющие упомянутый набор, называются Координатами вектора
; при этом числа, составляющие упомянутый набор, называются Координатами вектора ![]() .
.
Координаты N–мерного вектора ![]() можно расположить либо в строку
можно расположить либо в строку ![]() (Вектор–строка), либо в столбец (Вектор–столбец)
(Вектор–строка), либо в столбец (Вектор–столбец) 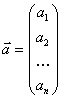 .
.
Определение
Два N–мерных вектора Равны Тогда и только тогда, когда Равны их соответствующие координаты, т. е. ![]() , если
, если ![]() ,
, ![]() .
.
Определение
Суммой двух N–мерных векторов называется вектор ![]() , компоненты которого равны сумме соответствующих компонент слагаемых векторов, т. е.,
, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т. е., ![]() ,
, ![]() .
.
Определение
Произведением N–мерного вектора ![]() на действительное число L называется вектор
на действительное число L называется вектор ![]() , компоненты которого равны произведению L на соответствующие компоненты вектора
, компоненты которого равны произведению L на соответствующие компоненты вектора ![]() , т. е.,
, т. е., ![]() ,
, ![]() .
.
Линейные операции над N–мерными векторами удовлетворяют следующим свойствам:
![]() – перемести тельное свойство;
– перемести тельное свойство;
![]() – сочетательное свойство;
– сочетательное свойство;
![]() – сочетательное относительно числового множителя свойство;
– сочетательное относительно числового множителя свойство;
![]() – распределительное относительно суммы векторов свойство;
– распределительное относительно суммы векторов свойство;
![]() – распределительное относительно суммы числовых множителей свойство;
– распределительное относительно суммы числовых множителей свойство;
Существует нулевой вектор ![]() такой, что
такой, что ![]() для любого вектора
для любого вектора ![]() .
.
Для любого вектора ![]() существует противоположный вектор
существует противоположный вектор ![]() такой, что
такой, что ![]() ;
;
![]() для любого вектора
для любого вектора ![]() .
.
Определение
Совокупность ![]() –мерных векторов, для которых определены операции Сложения векторов и Умножения вектора на число, и удовлетворяющих приведенным выше свойствам, называется Линейным векторным пространством
–мерных векторов, для которых определены операции Сложения векторов и Умножения вектора на число, и удовлетворяющих приведенным выше свойствам, называется Линейным векторным пространством ![]() .
.
| < Предыдущая | Следующая > |
|---|