6.3. Производная в данном направлении. Градиент
Производная функции ![]() В точке
В точке ![]() в направлении
в направлении ![]() , где
, где ![]() , определяется соотношением:
, определяется соотношением:
![]() ,
,
Где ![]() и
и ![]() - значения функции
- значения функции ![]() в точках
в точках ![]() и
и ![]() .
.
Если функция ![]() имеет частные производные, то справедлива формула:
имеет частные производные, то справедлива формула:
![]() , (5)
, (5)
Где ![]() - угол, образованный вектором
- угол, образованный вектором ![]() с осью
с осью ![]() .
.
Аналогично определяется производная в данном направлении ![]() для функции трех аргументов
для функции трех аргументов ![]() . В этом случае:
. В этом случае:
![]() , (6)
, (6)
Где ![]() - углы между вектором
- углы между вектором ![]() и соответствующими координатными осями.
и соответствующими координатными осями.
Градиентом функции ![]() В точке
В точке ![]() называется вектор, проекциями которого на координатные оси являются соответствующие частные производные данной функции:
называется вектор, проекциями которого на координатные оси являются соответствующие частные производные данной функции:
![]() . (7)
. (7)
Аналогично определяется градиент функции трех переменных ![]() :
:
![]() . (8)
. (8)
Задание 1. Найти производную функции ![]() в точке
в точке ![]() в направлении вектора
в направлении вектора ![]() .
.
Решение. Найдем частные производные данной функции и их значения в точке ![]() :
:

Определим теперь значения направляющих косинусов вектора ![]() :
:


![]()
![]()
![]()
 .
.
Применяя формулу (6), получим:
![]() .
.
Задание 2. Для функций ![]() и
и ![]() найти угол между
найти угол между ![]() и
и ![]() в данной точке
в данной точке 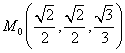 .
.
Решение. Вычислим частные производные данных функций и их значения в точке ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Тогда в силу формулы (8):

Найдем теперь угол ![]() между градиентами функций. По формуле для косинуса угла между векторами имеем:
между градиентами функций. По формуле для косинуса угла между векторами имеем:
![]() ,
,
Следовательно, угол между ![]() и
и ![]() в данной точке
в данной точке ![]() равен
равен ![]() .
.
| < Предыдущая | Следующая > |
|---|