6.2. Частные производные. Дифференциал функции

Частной производной функции по переменной В точке называется предел:

, (3)

Где - приращение аргумента . Аналогично определяется Частная производная функции по Переменной в точке :

, (4)

Где - приращение аргумента . Частные производные функции по переменной обозначают различными способами, например:

Аналогично частные производные функции по переменной обозначают следующим образом:

Заметим, что в силу определения частной производной все правила и формулы дифференцирования, введенные для функции одной переменной, сохраняются. Следует лишь помнить, что во всех этих правилах и формулах при нахождении частной производной по какому-либо аргументу все остальные аргументы считаются постоянными.

Частные производные и функции также являются функциями двух переменных и . Поэтому эти функции, в свою очередь, могут иметь частные производные, которые называются Частными производными второго порядкаИсходной Функции и обозначаются следующим образом:

- Вторая частная Производная функции По переменной ;

- вторая частная Производная функции По переменной ;

- Смешанные производные второго порядка функции .

Выражение

Называется полным приращением Функции в точке , а выражение

- полным дифференциалом Функции .

Аналогичные формулы имеют место и для функции трех переменных .

Задание. Показать, что функция удовлетворяет уравнению:

.

Решение. Найдем соответствующие частные производные, входящие в данное уравнение:

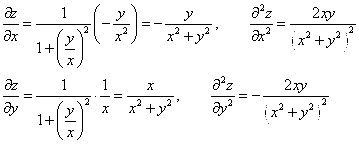
Подставим полученные значения частных производных второго порядка от функции в исходное уравнение. Получим:

.

Следовательно, функция удовлетворяет данному уравнению.

< Предыдущая		Следующая >