3.3. Непрерывность функции

Функция называется Непрерывной в точке , если:

1) эта функция определена в некоторой окрестности точки

2)

3) .

Теорема. Для того чтобы функция была непрерывна в точке , необходимо и достаточно, чтобы выполнялись равенства: .

Точка называется Точкой разрыва Непрерывности функции, если в этой точке функция не является непрерывной, т. е. если в этой точке нарушается хотя бы одно из условий определения непрерывности функции.

Если существуют конечные односторонние пределы , причем не все три числа равны между собой, то называется Точкой разрыва Первого рода. В частности, если:

1) , то называется Устранимой точкой разрыва;

2) , то называется Точкой разрыва типа скачка, причем разность называется Скачком функции в точке .

Точки разрыва функции, не являющиеся точками разрыва первого рода, называются Точками разрыва второго рода.

Справедливо следующее утверждение.

Задание 2. Задана функция

Исследовать функцию на непрерывность. Сделать чертеж.

Решение Функция задана различными непрерывными аналитическими выражениями для различных областей изменения аргумента . Следовательно, точками разрыва данной функции могут быть только те точки, в которых меняются аналитические выражения функции, т. е. точки И . Определим значения функции и ее односторонние пределы в этих точках:

1) :

.

Так как , то в точке функция непрерывна.

2) :

Так как , то точка является точкой разрыва непрерывности функции первого рода типа скачка.

Скачок функции в точке разрыва равен: =2. График функции представлен на рисунке:

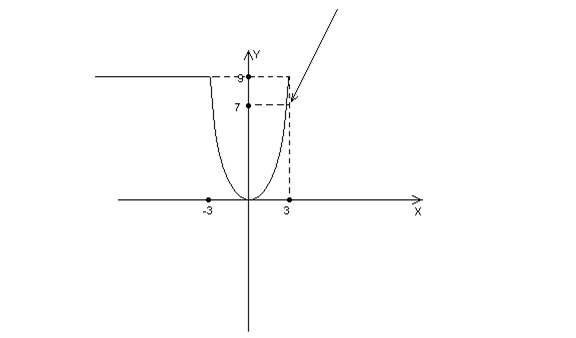
< Предыдущая		Следующая >