3.2. Предел функции
Пусть функция ![]()
![]() определена на множестве
определена на множестве ![]() . Число А называется Пределом функции
. Число А называется Пределом функции ![]() при
при ![]() , если
, если ![]()
![]() , что
, что ![]() при
при ![]()
![]() .
.
Это записывают так:
![]() .
.
Если ![]() и
и ![]() , то используют запись
, то используют запись ![]() ; если
; если ![]() и
и ![]() , то
, то ![]() .
.
Числа ![]() и
и ![]() называются соответственно Левосторонним и правосторонним пределами функции
называются соответственно Левосторонним и правосторонним пределами функции ![]() в точке
в точке ![]() .
.
Если существуют пределы ![]() и
и ![]() , то:
, то:
1) ![]() , где
, где ![]() ;
;
2) ![]() ;
;
3) ![]()

![]() .
.
При решении задач полезно знать следующие “замечательные” пределы:
1) ![]() 2)
2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
5) ![]()
Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида ![]() ,
,![]() ,
,![]() ,
,![]() , и т. д.
, и т. д.
Существуют различные приемы раскрытия данных неопределенностей:
Деление числителя и знаменателя на старшую степень переменной (при ![]() ); сокращение на множитель, создающий неопределенность; применение “замечательных” пределов и т. п.
); сокращение на множитель, создающий неопределенность; применение “замечательных” пределов и т. п.
Задание 1. Найти пределы функций, не пользуясь правилом Лопиталя.
1) ![]()
Решение. При ![]() получаем неопределенность вида
получаем неопределенность вида ![]() . Чтобы найти предел данной дробно - рациональной функции, необходимо предварительно разделить числитель и знаменатель дроби на
. Чтобы найти предел данной дробно - рациональной функции, необходимо предварительно разделить числитель и знаменатель дроби на ![]() , т. к. степень
, т. к. степень ![]() - наивысшая степень многочленов, определяющих данную рациональную функцию. Применяя основные теоремы о пределах и свойства бесконечно малых величин, получаем:
- наивысшая степень многочленов, определяющих данную рациональную функцию. Применяя основные теоремы о пределах и свойства бесконечно малых величин, получаем:
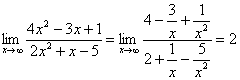
2) ![]()
Решение. Непосредственная подстановка предельного значения аргумента ![]() приводит к неопределенности вида
приводит к неопределенности вида ![]() . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму
. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму ![]()
![]()
3) ![]()
Решение Здесь имеет место неопределенность вида ![]() . Вычисление данного предела основано на применении первого “ замечательного” предела (
. Вычисление данного предела основано на применении первого “ замечательного” предела (![]() ).Имеем:
).Имеем: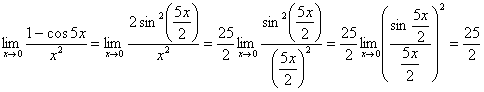
4) ![]()
Решение. При ![]() данная функция представляет собой степень, основание которой стремится к 1, а показатель – к
данная функция представляет собой степень, основание которой стремится к 1, а показатель – к ![]() (неопределенность вида
(неопределенность вида ![]() ). Преобразуем функцию так, чтобы использовать второй “замечательный” предел (
). Преобразуем функцию так, чтобы использовать второй “замечательный” предел (![]() ). Получим:
). Получим:
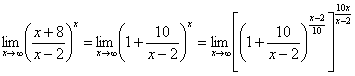 .
.
Так как ![]() при
при ![]() ,то
,то 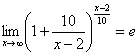 . Учитывая, что
. Учитывая, что ![]() , находим
, находим ![]() .
.
| < Предыдущая | Следующая > |
|---|