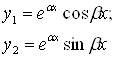46. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение вида , где ‑ некоторые действительные числа, называется Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.

Теорема. Если и ‑ частные решения уравнения , то есть общее решение этого уравнения.

Для определения частных решений и следует предварительно решить Характеристическое уравнение:

.

При решении данного квадратного уравнения возможны три случая:

Корни характеристического уравнения	Частные решения	Общее решение
1. Действительные разные и
2. Действительные равные
3. Комплексно-сопряженные

Пример 12. Найти общее решение дифференциального уравнения .

Составим характеристическое уравнение: . Корни этого уравнения различные и действительные и , поэтому ‑ частные решения этого уравнения, тогда ‑ общее решение данного уравнения.

Пример 13. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: .

Корни характеристического уравнения ‑ действительные и равные: , поэтому частные решения ‑ . Тогда общее решение уравнения: .

Для определения частного решения в равенства и подставим начальные условия.

Получим: .

Подставив эти значения в общее решение, найдем частное: .

Пример 14. Найти общее решение дифференциального уравнения .

Корни характеристического уравнения комплексно-сопряженные: . В этом случае . Общее решение будет: .

< Предыдущая		Следующая >