45. Задача Коши
Множество решений дифференциального уравнения второго порядка определяется двумя произвольными постоянными. Чтобы выделить единственное решение уравнения, достаточно задать значение функции и ее производной при фиксированном значении аргумента.
Задача нахождения решения дифференциального уравнения, удовлетворяющего условиям: 
, где 
‑ заданные числа, называется Задачей Коши. Эти условия часто называют начальными условиями, так как с экономической точки зрения они означают, что в фиксированный момент времени задано начальное состояние экономического процесса и скорость его изменения.
Геометрический смысл задачи Коши состоит в нахождении интегральной кривой, проходящей через заданную точку и имеющей заданный угловой коэффициент касательной в этой точке.
Пример 11. Решить задачу Коши 
.
Найдем все решения данного уравнения. Интегрируем: 
, 
.
Воспользовавшись начальными условиями, определим значение констант 
и 
из системы уравнений:
.
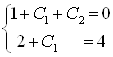Следовательно, 
, 
и искомое решение:
.
| < Предыдущая | Следующая > |
|---|
