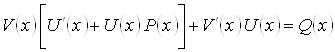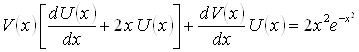43. Линейные дифференциальные уравнения

Уравнение вида

,

(2)

Где и непрерывные функции от называется Линейным, в частности, уравнение называется линейным без правой части или Линейным однородным.

В линейном однородном уравнении переменные разделяются: 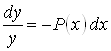и поэтому его интегрирование сводится к вычислению интегралов от обеих частей равенства: .

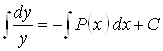Для того, чтобы решить уравнение (2) при будем искать неизвестную функцию в виде произведения двух пока неизвестных функций от , т. е. положим тогда .

Подставить значения и в уравнение (2):

.

После группировки получим:

(2')

Выберем так, чтобы выражение, стоящее в квадратных скобках, обращалось в ноль, т. е. . Для этого достаточно, чтобы было частным решением уравнения с разделяющимися переменными:

или .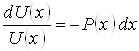

Проинтегрировав его, берем частное решение, отвечающее значению . Находим . Подставив в уравнение (2') значение , получим второе дифференциальное уравнение с разделяющимися переменными:

, или ,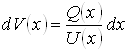

Общее решение которого .

Следовательно, общим решением уравнения (2) будет .

В ряде случаев дифференциальное уравнение первого порядка является линейным не относительно , а относительно , т. е. может быть приведено к виду: .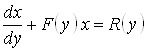

Метод интегрирования его тот же, что и для уравнения (2), но переменные и меняют свои роли: считается аргументом, а ‑ неизвестной функцией.

Пример 8. Проинтегрировать дифференциальное уравнение:

.

Положим , тогда .

Подставим и в данное уравнение:

;

(3)

Положим , или .

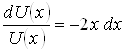Проинтегрировав, получим частное решение при :

или .

При равенство (3) обратится в уравнение:

;

,

Откуда и общим решением данного уравнения будет .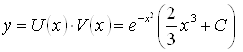

Решение многих дифференциальных уравнений нельзя свести к интегрированию известных функций. Поэтому большое значение имеют различные приближенные методы интегрирования уравнений.

< Предыдущая		Следующая >