42. Однородные дифференциальные уравнения

Дифференциальное уравнение, которое может быть преобразовано к виду 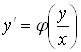называет Однородным.

Подстановка , где ‑ новая неизвестная функция, приводит однородное уравнение к уравнению с разделяющимися переменными.

Если , то и . Подставляя в уравнение, получим:, т. е. или .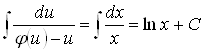

После интегрирования подставим вместо и получим общий интеграл данного уравнения.

Пример 7. Проинтегрировать уравнение .

Разделив обе части равенства на , получим уравнение, правая часть которого есть функция отношения :

.

Положив в нем и , получим уравнение с разделяющимися переменными:

.

Разделяем переменные: .

Интегрируя и подставляя вместо , получим общий интеграл исходного уравнения:

;

;

.

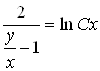< Предыдущая		Следующая >