41. Лекция 27. Дифференциальные уравнения с разделяющимися переменными

Если уравнение вида после преобразования может быть записано в виде , то оно называется Уравнением с Разделяющимися переменными.

Исключим из рассмотрения точки, в которых и . Тогда разделим обе части уравнения на , получим:

,

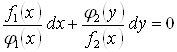В котором переменные разделены.

Общим интегралом уравнения будет:

.

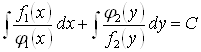Пример 5. Найти общий интеграл уравнения и выделить интегральную кривую, проходящую через точку .

Общим интегралом будет Или .

Полагая в нем , находим, что . Искомой интегральной кривой будет .

Пример 6. Найти общий интеграл

Разделим переменные в данном уравнении, деля обе части на :

.

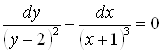Почленно интегрируя, получим:

;

;

.

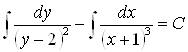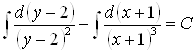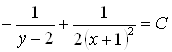< Предыдущая		Следующая >