40. Задача Коши

Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, которое при заданном значении аргумента принимает заданное значение , т. е. удовлетворяет начальному условию .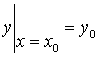

Геометрически задача Коши формулируется следующим образом: среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через заданную точку . Решение задачи Коши называют Частным решением дифференциального уравнения.

Пример 4. Найти:

1) семейство кривых, для которых угловой коэффициент касательной равен ординате точки касания;

2) кривую этого семейства, проходящую через точку .

Решение.

1) Дифференциальное уравнение искомого семейства или .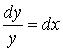

2) Проинтегрировав обе части равенства, получим: , откуда ‑ уравнение семейства кривых, обладающих заданным свойством.

Определим значение , соответствующее начальным значениям: , т. е. .

Следовательно, ‑ искомая интегральная кривая.

< Предыдущая		Следующая >