37. Лекция 26. Дифференциальные уравнения. Основные понятия

Главная цель менеджера, изучающего какой-либо экономический процесс, заключается в выявлении его закономерности, в получении аналитического выражения функциональной зависимости между переменными параметрами этого процесса.

Большинство таких задач на отыскание связи между переменными сводится к решению уравнений, содержащих производные или дифференциалы неизвестных функций. Такие уравнения называют Дифференциальными.

Огромное значение этих задач для практики, как и в теории обуславливает особо важное значение этого раздела математического анализа.

Порядком дифференциального уравнения называется порядок высшей производной, содержащейся в этом уравнении.

Дифференциальным уравнением первого порядка называется уравнение вида:

,

(1)

Где ‑ аргумент; ‑ неизвестная функция.

Наиболее простым является дифференциальное уравнение, разрешенное относительно :

.

Иногда уравнение первого порядка записывается в форме:

.

Функция называется решением уравнения (1), если она обращает его в тождество, т. е. .

Решение, заданное неявно, т. е. в виде , называется Интегралом дифференциального уравнения.

Пример 1. Показать, что уравнение , определяющее как неявную функцию от , есть интеграл дифференциального уравнения .

Дифференцируя данное уравнение, найдем :

.

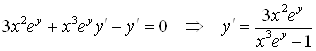Подставив в дифференциальное уравнение, получим тождество:

.

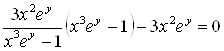< Предыдущая		Следующая >