38. Дифференциальные уравнения семейства кривых
Однопараметрическим семейством кривых называется совокупность линий, определяемая уравнением ![]() .
.
Фиксируя значение параметра ![]() , получают конкретную линию данного семейства.
, получают конкретную линию данного семейства.
Например, уравнение ![]() определяет собой семейство парабол с вершиной в начале координат, симметричных относительно оси
определяет собой семейство парабол с вершиной в начале координат, симметричных относительно оси ![]() . Придавая параметру
. Придавая параметру ![]() значения, получают параболы
значения, получают параболы ![]() .
.
Дифференцируя уравнение семейства линий по ![]() (считая
(считая ![]() функцией от
функцией от ![]() ):
):
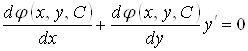
И исключая параметр ![]() , приходят к дифференциальному уравнению вида
, приходят к дифференциальному уравнению вида ![]() , которому удовлетворяет любая линия данного семейства.
, которому удовлетворяет любая линия данного семейства.
Пример 2. Из семейства окружностей ![]() выделить ту, которая проходит через точку
выделить ту, которая проходит через точку ![]() . Составить дифференциальное уравнение данного семейства окружностей.
. Составить дифференциальное уравнение данного семейства окружностей.
Чтобы выделить нужную окружность, необходимо найти соответствующее ей значение параметра ![]() . Так как искомая окружность проходит через точку
. Так как искомая окружность проходит через точку ![]() , то координаты этой точки удовлетворяют уравнению окружности. Подставляя
, то координаты этой точки удовлетворяют уравнению окружности. Подставляя ![]() , получим
, получим ![]() . Искомое уравнение имеет вид:
. Искомое уравнение имеет вид: ![]() .
.
Чтобы составить дифференциальное уравнение семейства окружностей ![]() , продифференцируем его по
, продифференцируем его по ![]() :
:
![]() или
или 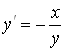 .
.
| < Предыдущая | Следующая > |
|---|