33. Положительные ряды
Среди числовых рядов выделяются ряды, все члены которых неотрицательны. Такие ряды называют положительными. У такого ряда последовательность ![]() его частных сумм является возрастающей и, поэтому, доя его сходимости достаточно, чтобы последовательность
его частных сумм является возрастающей и, поэтому, доя его сходимости достаточно, чтобы последовательность ![]() была ограниченной. Вывод о сходимости или расходимости положительного ряда может быть сделан на основании сравнения членов этого ряда с членами некоторого эталонного ряда, поведение которого (сходимость или расходимость) известно. Соответствующие теоремы называют Признаками сравнения. Приведем некоторые из них.
была ограниченной. Вывод о сходимости или расходимости положительного ряда может быть сделан на основании сравнения членов этого ряда с членами некоторого эталонного ряда, поведение которого (сходимость или расходимость) известно. Соответствующие теоремы называют Признаками сравнения. Приведем некоторые из них.
Будем рассматривать два положительных ряда
|
|
(4) |
|
|
(5) |
1°. Пусть существует номер ![]() такой, что
такой, что ![]() .
.
Если ряд (5) сходится, то сходится и ряд (4). Если ряд (4) расходится, то расходится и ряд (5).
Пример 4. Рассмотрим ряд 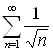 . Сравним этот ряд с гармоническим рядом
. Сравним этот ряд с гармоническим рядом ![]() . Так как
. Так как ![]() , то ряд
, то ряд 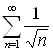 расходится.
расходится.
Пример 5. Рассмотрим ряд 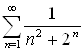 . Сравним его со сходящимся геометрическим рядом
. Сравним его со сходящимся геометрическим рядом ![]() . Поскольку
. Поскольку ![]() , то ряд
, то ряд 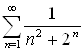 сходится.
сходится.
2°. Пусть существует конечный или бесконечный предел 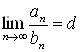 .
.
A). Если ![]() , то из сходимости ряда (5) следует сходимость ряда (4).
, то из сходимости ряда (5) следует сходимость ряда (4).
B). Если ![]() , то из расходимости ряда (5) следует расходимость ряда (4).
, то из расходимости ряда (5) следует расходимость ряда (4).
Пример 6. Рассмотрим ряд 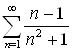 . Сравним его с гармоническим рядом. Поскольку
. Сравним его с гармоническим рядом. Поскольку ![]() при
при ![]() , то ряд
, то ряд 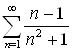 расходится.
расходится.
Пример 7. Рассмотрим ряд 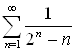 . Сравним его со сходящимся геометрическим рядом
. Сравним его со сходящимся геометрическим рядом ![]() . Так как
. Так как 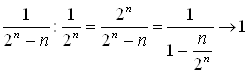 при
при ![]() , то ряд
, то ряд 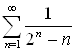 сходится.
сходится.
Для положительных рядов доказаны признаки, позволяющие сделать вывод о сходимости или расходимости ряда, изучая поведение при ![]() его
его ![]() -го члена.
-го члена.
Признак Даламбера. Пусть существует предел  .
.
Если ![]() , то ряд
, то ряд ![]() сходится.
сходится.
Если ![]() , то ряд
, то ряд ![]() расходится.
расходится.
Пример 8. Рассмотрим ряд ![]() . Для этого ряда
. Для этого ряда 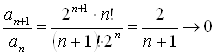 при
при ![]() . По признаку Даламбера ряд сходится.
. По признаку Даламбера ряд сходится.
Пример 9. Рассмотрим ряд ![]() . Для этого ряда
. Для этого ряда 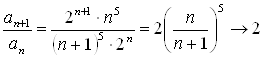 при
при ![]() . По признаку Даламбера ряд расходится.
. По признаку Даламбера ряд расходится.
Признак Коши. Пусть существует предел ![]() .
.
Если ![]() , то ряд
, то ряд ![]() сходится.
сходится.
Если ![]() , то ряд
, то ряд ![]() расходится.
расходится.
Пример 10. Рассмотрим ряд 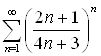 . Для этого ряда
. Для этого ряда 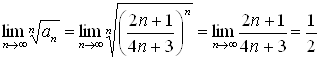 По признаку Коши ряд сходится.
По признаку Коши ряд сходится.
Пример 11. Рассмотрим ряд  . Для этого ряда
. Для этого ряда 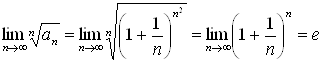 . Значит, ряд расходится.
. Значит, ряд расходится.
Заметим, то признаки Даламбера и Коши не дают ответа, когда ![]() или
или ![]() . В этом случае можно исследовать ряд с помощью других признаков.
. В этом случае можно исследовать ряд с помощью других признаков.
Интегральный признак. Пусть ![]() ‑ положительная неубывающая функция, такая что
‑ положительная неубывающая функция, такая что ![]() . Если последовательность
. Если последовательность ![]() ,
, 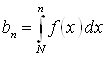 Сходится, то сходится и ряд
Сходится, то сходится и ряд ![]() . Если последовательность
. Если последовательность ![]() расходится, то расходится и исходный ряд.
расходится, то расходится и исходный ряд.
Пример 12. Рассмотрим ряд ![]() (этот ряд называют Обобщенным Гармоническим рядом).
(этот ряд называют Обобщенным Гармоническим рядом).
Функция ![]() убывающая, положительная и
убывающая, положительная и ![]() ,
, ![]() ,
, 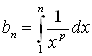 .
.
Если ![]() , то
, то 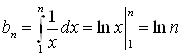 . Так как
. Так как ![]() при
при ![]() , то последовательность
, то последовательность ![]() расходится, значит, расходится и ряд. Впрочем, при
расходится, значит, расходится и ряд. Впрочем, при ![]() исследуемый ряд – гармонический, и его расходимость была доказана ранее.
исследуемый ряд – гармонический, и его расходимость была доказана ранее.
Если ![]() , то
, то  .
.
При ![]() ,
,  ; при
; при ![]()
 . Таким образом, последовательность
. Таким образом, последовательность ![]() сходится при
сходится при ![]() и расходится при
и расходится при ![]() .
.
Вывод. Обобщенный гармонический ряд сходится при ![]() и расходится при
и расходится при ![]() .
.
Пример 13. Рассмотрим ряд 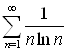 .
.
Функция ![]() ;
;
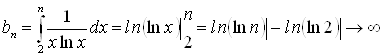 при
при ![]() .
.
Значит, ряд расходится.
Если в признаке сравнения 2° в качестве эталонного использовать обобщенный гармонический ряд, то можно получить так называемый Степенной признак сходимости положительных рядов. Этот признак дает ответ на вопрос о сходимости ряда в некоторых случаях, когда признаки Коши и Даламбера ответа не дают.
Степенной признак. Пусть ![]() при
при ![]() , где
, где ![]() . Тогда при
. Тогда при ![]() ряд расходится. При
ряд расходится. При ![]() ряд сходится (условие
ряд сходится (условие ![]() равносильно тому, что
равносильно тому, что 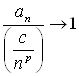 при
при ![]() . Говорят, что
. Говорят, что ![]() эквивалентен
эквивалентен ![]() при
при ![]() ).
).
Пример 14. Рассмотрим ряд 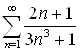 . Для этого ряда
. Для этого ряда 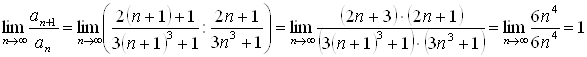 , значит, признак Даламбера не дает ответа на вопрос о сходимости ряда. Можно убедиться, что и признак Коши не приведет к желаемому результату.
, значит, признак Даламбера не дает ответа на вопрос о сходимости ряда. Можно убедиться, что и признак Коши не приведет к желаемому результату.
В то же время, ![]() эквивалентен
эквивалентен ![]() , так как
, так как 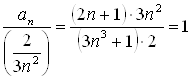 при
при ![]() . Значит, в этом случае
. Значит, в этом случае ![]() и, следовательно, ряд сходится по степенному признаку.
и, следовательно, ряд сходится по степенному признаку.
Пример 15. Ряд 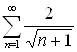 имеет
имеет ![]() -й член
-й член ![]() , который эквивалентен
, который эквивалентен ![]() . Значит, ряд расходится.
. Значит, ряд расходится.
| < Предыдущая | Следующая > |
|---|