34. Лекция 25. Знакочередующиеся ряды

Ряд вида

(6)

Называют знакочередующимся.

Признак Лейбница. Если последовательность стремится к нулю монотонно то ряд (6) сходится.

Пример 16. Рассмотрим ряд 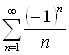. Для него , причем, , т. е. последовательность монотонно убывает и . Поэтому ряд сходится.

Для исследования монотонности последовательности удобно ввести некоторую вспомогательную (дифференцируемую) функцию такую, что , и исследовать функцию на монотонность, воспользовавшись критерием монотонности дифференцируемой функции.

Пример 17. Для ряда 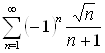последовательность при . Для исследования монотонности последовательности рассмотрим вспомогательную функцию 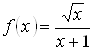. Заметим, что . Поскольку . Для функция убывает. Значит, , т. е. . Значит. последовательность убывает и . По признаку Лейбница ряд сходится.

< Предыдущая		Следующая >