32. Лекция 24. Ряды. Основные понятия

Пусть ‑ последовательность действительных чисел. Рассмотрим последовательность , построенную следующим образом:

;

;

;

;

Последовательность удобно записывать в виде . Такую последовательность называют Числовым рядом. Числа называют Членами или Элементами ряда. Числовой ряд задают обычно перечислением его элементов или указанием формулы, с помощью которой для заданного можно вычислить -й член ряда.

Пример 1. Ряд имеет -й член .

Поэтому

Т. е. .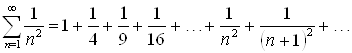

Рассмотрим ряд

(1)

Сумму 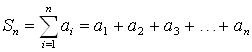называют -й Частной Суммой ряда (1). Если последовательность частных сумм ряда (1) сходится, то ряд (1) называют Сходящимся, а число называют суммой ряда. Если же последовательность не имеет конечного предела, то ряд (1) называют Расходящимся.

Пример 2. Рассмотрим ряд 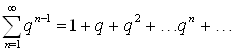. Для него , что представляет собой сумму первых членов геометрической прогрессии.

Если , то и .

Если , то и .

Если , то и .

Если , то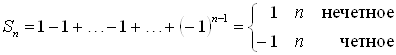

И не существует.

Таким образом, ряд 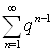при сходится и расходится при . Этот ряд называется Геометрическим.

Пусть ряд (1) сходится и ‑ его сумма. Поскольку

,

(2)

То при получаем .

Откуда следует Необходимое условие сходимости ряда: если ряд сходится, то

.

(3)

Если условие (3) не выполнено. То ряд расходится.

Пример 3. Ряд 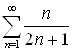расходится, т. к. и .

Условие (3) не является достаточным для сходимости рядя. Даже если оно выполнено, ряд может расходится. Покажем это на примере Гармонического ряда . Для этого ряда при , т. е. условие (3) выполнено. В то же время,

,

.

Поэтому .

Предположим, что гармонический ряд сходится и ‑ его сумма, т. е. при . Поскольку , то при получаем ‑ противоречие. Значит, предположение о сходимости гармонического ряда было неверным.

Несколько первых членов ряда не влияют на его сходимость. Если у ряда (1) удалить несколько первых членов, то получим ряд , называемый остатком ряда (1). Сходимость ряда равносильна сходимости его любого остатка.

< Предыдущая		Следующая >