18. Локальный экстремум

Необходимое условие локального экстремума. Если дифференцируемая функция имеет локальный экстремум в точке , то в этой точке должны выполняться условия:

.

Точки, в которых выполнены условия (1), называют Стационарными точками.

Исследование стационарных точек. Для исследования стационарных точек вычисляют

И составляют матрицу , .

Обозначим 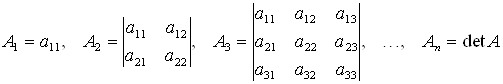– главные Миноры матрицы .

Если , то C – точка локального минимума.

Если , то C – точка локального максимума.

В частности, для функции , пусть

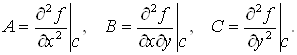
Если , то в точке C экстремума нет.

Если , то экстремум есть, причем, если , имеет место локальный минимум, а если – локальный максимум.

< Предыдущая		Следующая >
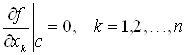