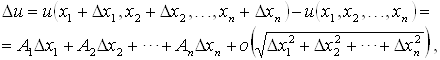16. Лекция 16. Функции нескольких переменных
Будем рассматривать упорядоченные наборы ![]() чисел
чисел ![]() . Такие наборы называют Точками. Точки можно складывать и умножать на число.
. Такие наборы называют Точками. Точки можно складывать и умножать на число.
Так, если ![]() , то:
, то:
![]() ,
,
![]() .
.
Множество всех таких точек образует ![]() -мерное арифметическое пространство
-мерное арифметическое пространство ![]() . При
. При ![]() получаем плоскость. При
получаем плоскость. При ![]() ‑ обычное 3-х мерное пространство.
‑ обычное 3-х мерное пространство.
Расстоянием между точками ![]() и
и ![]() будем называть число
будем называть число
![]() .
.
При ![]() и
и ![]() ‑ это обычное расстояние между точками на плоскости или в пространстве.
‑ это обычное расстояние между точками на плоскости или в пространстве.
Пусть ![]() и каждой точке
и каждой точке ![]() по закону
по закону ![]() ставится в соответствие число
ставится в соответствие число ![]() (единственное, определяемое по закону
(единственное, определяемое по закону ![]() ). Тогда говорят, что на
). Тогда говорят, что на ![]() задана функция
задана функция ![]() переменных
переменных ![]()
![]() .
.
Если ![]() определена формулами, то Областью определения
определена формулами, то Областью определения ![]() называют множество точек
называют множество точек ![]() , для которых эти формулы имеют смысл.
, для которых эти формулы имеют смысл.
Число ![]() называют Пределом Функции
называют Пределом Функции ![]() в точке
в точке ![]() , если
, если ![]() такое, что
такое, что ![]() . Обозначение:
. Обозначение: ![]()
Функцию ![]() называют Непрерывной в точке
называют Непрерывной в точке ![]() , если
, если ![]() .
.
Для непрерывных функций ![]() переменных справедливо большинство теорем, сформулированных для непрерывных функций одной переменной.
переменных справедливо большинство теорем, сформулированных для непрерывных функций одной переменной.
В точке ![]() дадим переменной точке
дадим переменной точке ![]() приращение
приращение ![]() . При этом функция
. При этом функция ![]() получит приращение:
получит приращение:![]() .
.
Если ![]() при
при ![]() , то
, то ![]() непрерывна в точке
непрерывна в точке ![]() .
.
Функция ![]() называется Дифференцируемой в точке
называется Дифференцируемой в точке ![]() , если ее приращение в этой точке можно представить в виде:
, если ее приращение в этой точке можно представить в виде:
|
|
(1) |
Где ![]() – постоянные (они зависят от
– постоянные (они зависят от ![]() ), Называемые частными производными. Их обозначают:
), Называемые частными производными. Их обозначают:
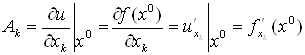 .
.
При практическом вычислении частных производных используют те же правила, что и при вычислении производных функций одной переменной. При этом, вычисляя ![]() , все переменные, кроме
, все переменные, кроме ![]() , воспринимают как постоянные.
, воспринимают как постоянные.
Частные производные высших порядков определяют последовательно:
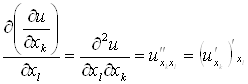 .
.
Если ![]() , то обозначают
, то обозначают 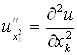 .
.
Аналогично определяют 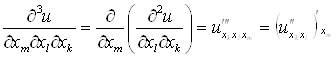 и так далее.
и так далее.
Главную часть приращения функции (1)
![]()
Называют Дифференциалом функции и обозначают ![]() . Если
. Если ![]() – независимые переменные, то
– независимые переменные, то
![]() .
.
Тогда, 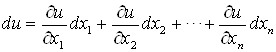 .
.
Дифференциалы высших порядков определяют последовательно ![]() И т. д.
И т. д.
Полагают ![]() .
.
Для функции двух переменных ![]() имеем:
имеем:
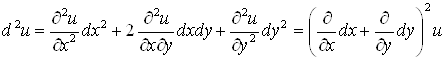 .
.
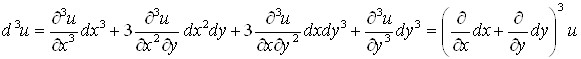 .
.
Аналогично 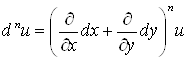 .
.
Если ![]() , то
, то 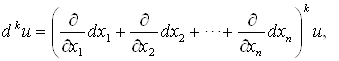
![]()
Если функция имеет в точке ![]() непрерывные частные производные до порядка
непрерывные частные производные до порядка ![]() включительно, то ее значение в точке
включительно, то ее значение в точке ![]() можно представить в виде
можно представить в виде
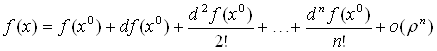 ,
,
где ![]() .
.
Эту формулу называют Формулой Тейлора.
(Примеры решения задач см. А. С. Гринберг и др. "Математика для менеджера" Практикум, § 20).
| < Предыдущая | Следующая > |
|---|