08. Исследование стационарных точек

I правило. Если при возрастании при переходе через стационарную точку производная меняет знак с + на ‑ , то ‑ точка локального максимума. Если меняет знак с ‑ на + , то ‑ точка локального минимума функции . Если не меняет знак в точке , то экстремума нет.

II правило. Если вторая производная в стационарной точке положительная, то ‑ точка локального минимума функции . Если вторая производная в стационарной точке отрицательная, то ‑ точка локального максимума функции .

Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по I правилу. Экстремум в такой точке называется Острым экстремумом.

Пример 2. Найти экстремум функции .

.

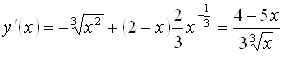Функция имеет стационарную точку (в этой точке производная равна нулю). В точке производная обращается в бесконечность.

Поскольку при и при 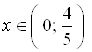, то функция имеет в точке локальный минимум . Это будет острый минимум.

При переходе через стационарную точку производная меняет знак с ‑ на + , значит функция имеет локальный максимум .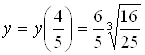

< Предыдущая		Следующая >