02. Правила дифференцирования. Таблица производных
Будем считать, что функции ![]() дифференцируемы, т. е. имеют производные
дифференцируемы, т. е. имеют производные ![]() . Тогда:
. Тогда:
1°. Функция ![]() дифференцируема и
дифференцируема и ![]() .
.
2°. Если ![]() ‑ постоянная, то функция
‑ постоянная, то функция ![]() дифференцируема и
дифференцируема и ![]() .
.
3°. Из 1° и 2° следует, что ![]() .
.
4°. Функция ![]() дифференцируема и
дифференцируема и ![]() .
.
5°. Из 4° следует, что ![]() .
.
6°. Если ![]() определена и дифференцируема, то
определена и дифференцируема, то  .
.
Основные элементарные функции дифференцируемы всюду, где они определены. Производные этих функций могут быть вычислены по определению, т. е. по формуле:
![]()
И с помощью правил дифференцирования.
Полученные значения производных основных элементарных функций приведем в таблице.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Использование таблицы производных и правил дифференцирования позволяет вычислять производные арифметических комбинаций основных элементарных функций.
Пример 1. 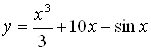 . Вычислить
. Вычислить ![]() .
.
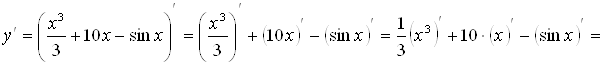
![]() .
.
Пример 2.  . Вычислить
. Вычислить ![]() .
.
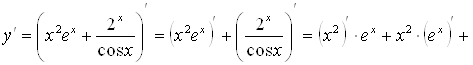
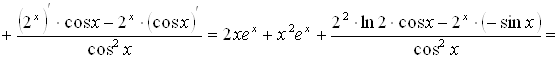
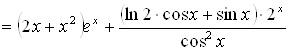 .
.
Пример 3. ![]() . Вычислить
. Вычислить ![]() .
.
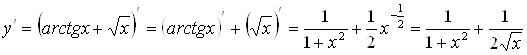 .
.
| < Предыдущая | Следующая > |
|---|
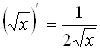
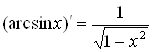 ;
;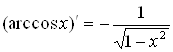 .
.