5.11.8 Нахождение производной матрицы
В зависимости от строения множеств 
и 
различают четыре класса отображений (функций).
I. 
– скалярная функция скалярного аргумента, 
и 
, то есть 
, следовательно, матрица 
имеет размер 
и состоит из одного элемента, равного 
. Этот случай рассмотрен в теме «дифференциальное исчисление функции одного аргумента».
II. Функцию 
(или большего числа переменных), где 
– независимые переменные, называют скалярной функцией векторного аргумента 
(см. 5.11.1).
Тогда 
, следовательно, – матрица размера 
имеет вид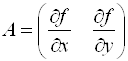 
. Если у функции 
аргументов больше двух, например 
, то есть 
, то 
.
III. Функцию 
называют векторной функцией скалярного аргумента 
. Тогда 
и производная матрица имеет размер 
. Можно записать
.
IV. Векторную функцию векторного аргумента можно записать так:
.
Видим, что вектор 
имеет 
координат, а 
– 
координат, то есть 
и матрица 
имеет размер 
.
.
| < Предыдущая | Следующая > |
|---|
