5.11.9 Производная композиция отображений
Композиция – общее название для операции, ставящей в соответствие двум упорядоченным элементам ![]() и
и ![]() некоторого множества третий элемент
некоторого множества третий элемент ![]() . Обозначается
. Обозначается ![]() (или
(или ![]() ). В частности, составление сложной функции
). В частности, составление сложной функции ![]() является композицией (или суперпозицией) отображений.
является композицией (или суперпозицией) отображений.
Имеем: ![]() , тогда
, тогда ![]() .
.
Производная матрица композиции отображений равна произведению производных матриц исходных функций. Если обозначить матрицы ![]() , то
, то ![]() .
.
Рассмотрим случаи, уже разобранные нами в пункте 5.11.4.
I. Пусть ![]() , где
, где ![]() ,
, ![]() , тогда
, тогда ![]() . Найдем
. Найдем ![]() .
.
Матрица оператора ![]() , преобразующего
, преобразующего ![]() в
в ![]() имеет размер
имеет размер ![]() , то есть состоит из одной строки и двух столбцов
, то есть состоит из одной строки и двух столбцов 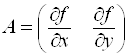 . Если обозначить
. Если обозначить ![]() , то получим вектор-функцию скалярного аргумента (см. пункт 5.11.8. случай III), тогда
, то получим вектор-функцию скалярного аргумента (см. пункт 5.11.8. случай III), тогда ![]() и матрица
и матрица 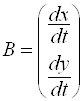 . Матрица оператора
. Матрица оператора ![]() композиции
композиции ![]() имеет размер
имеет размер ![]() и равна произведению матриц
и равна произведению матриц ![]() и
и ![]() :
: ![]()
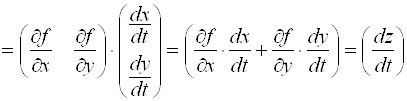 .
.
II. Пусть ![]() , где
, где ![]() , тогда
, тогда ![]() . Функция
. Функция ![]() осуществляет отображение
осуществляет отображение ![]() , тогда
, тогда 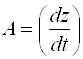 , а функция
, а функция ![]() переводит
переводит ![]() в
в ![]() и производная матрица
и производная матрица  . Матрица
. Матрица ![]() композиции отображений равна
композиции отображений равна ![]() и имеет размер
и имеет размер ![]() :
: 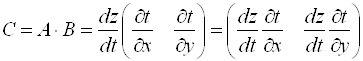 . Иначе
. Иначе  .
.
III. Рассмотрим случай ![]() , где
, где ![]() . Тогда
. Тогда ![]() . Имеем
. Имеем ![]() и
и 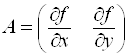 ;
; ![]() и
и  . Матрица композиции
. Матрица композиции
Отображений  .
.
Получили 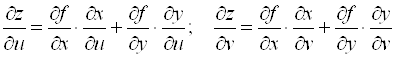 .
.
Перепишем примеры из 5.11.4 в новой интерпретации.
I. Отображение ![]() .
.
Пример 1. Дана функция ![]() , где
, где ![]() . Найти
. Найти ![]() .
.
Решение. 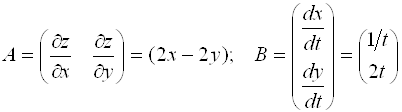 ;
;  или
или  .
.
Пример 2. ![]() , где
, где ![]() . Найти
. Найти ![]() .
.
Решение. 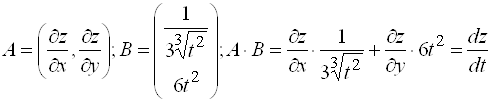 .
.
Пример 3. ![]() , где
, где ![]() . Найти
. Найти ![]() .
.
Решение.  ,
,
 ;
;  .
.
II. Отображение ![]() .
.
Пример 4.  .
.
Решение.  .
.
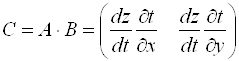 , то есть
, то есть 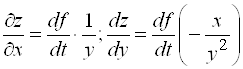 .
.
III. Отображение ![]() .
.
Пример 5.  .
.
Решение.
 .
.
 ;
; 
| < Предыдущая | Следующая > |
|---|