5.11.7 Понятие о производной матрице

Ранее (см. пункт 5.10.5) мы назвали функцию дифференцируемой в точке , если ее приращение можно представить в виде

, (1)

Где при .

Формулу (1) можно трактовать иначе, если функцию рассматривать как оператор или отображение одного множества на другое, а линейную функцию – как линейный оператор. Тогда дифференцирование отображения (нахождение дифференциала) это есть нахождение главной линейной части отображения, что означает аппроксимацию (замену, приближение) отображения в окрестности некоторой точки линейным отображением.

Всякую упорядоченную совокупность из вещественных чисел в -мерном евклидовом пространстве можно трактовать либо как «точку» с координатами , либо как вектор , являющегося радиус-вектором точки . Пространство называют точечно-векторным пространством, так как его элементы можно трактовать как точки или как векторы. Разумеется, здесь имеется в виду не геометрический вектор.

В формуле (1) теперь : , – линейный оператор: .

Разберемся в обозначениях. Если – обычная скалярная функция одного скалярного аргумента, то есть , то и точки (или числа) . Если же – произвольная функция (скалярная функция векторного аргумента , векторная функция скалярного аргумента, вектор-функция векторного аргумента), то и точки или векторы и тогда .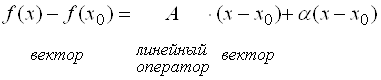

Иначе:

. (2)

Всякий линейный оператор определяется своей матрицей, то есть подействовать оператором на вектор это все равно, что матрицу этого оператора умножить на матрицу из координат вектора . Следовательно, (2) можно записать в виде:

. (3)

Матрицу в соотношении (3) называют производной матрицей и обозначают .

Таким образом, производная матрица – это матрица линейного оператора.

В курсе линейной алгебры было показано, что всякий линейный оператор имеет матрицу размера ( строк и столбцов), следовательно, производная матрица будет иметь такой же размер.

< Предыдущая		Следующая >