5.11.6 Экстремум функции двух переменных. Наибольшее и наименьшее значения
Понятие максимума и минимума можно распространить и на функции нескольких переменных (здесь для случая двух переменных).
Определение. Если в некоторой окрестности точки ![]() выполняется неравенство
выполняется неравенство ![]()
![]() , то говорят, что
, то говорят, что ![]() имеет максимум (минимум) в точке
имеет максимум (минимум) в точке ![]() .
.
Теорема. (Необходимое условие экстремума).
Если дифференцируемая ![]() имеет экстремум в точке
имеет экстремум в точке ![]() , то обе частные производные функции в этой точке равны нулю.
, то обе частные производные функции в этой точке равны нулю.
Точки, в которых обе частные производные функции ![]() обращаются в нуль, называются стационарными. Если не ограничиваться рассмотрением только дифференцируемых функций, то необходимое условие экстремума нужно дополнить.
обращаются в нуль, называются стационарными. Если не ограничиваться рассмотрением только дифференцируемых функций, то необходимое условие экстремума нужно дополнить.
Если ![]() имеет экстремум в точке
имеет экстремум в точке ![]() , то:
, то:
А) или обе частные производные равны нулю в точке ![]() ;
;
Б) или хотя бы одна из частных производных равна бесконечности или не существует в точке ![]() .
.
В подозрительных точках экстремума может и не быть (сравните с функцией одной переменной).
Теорема. (Достаточные условия экстремума).
Если в критической точке ![]() выполняется неравенство
выполняется неравенство ![]() , то функция
, то функция ![]() имеет в точке
имеет в точке ![]() экстремум, причем:
экстремум, причем:
А) если ![]() , то минимум;
, то минимум;
Б) если ![]() , то максимум.
, то максимум.
Если ![]() , то в точке
, то в точке ![]() нет экстремума;
нет экстремума;
Если ![]() , то экстремум может быть и может не быть (нужны дополнительные исследования).
, то экстремум может быть и может не быть (нужны дополнительные исследования).
Пример 1. Исследовать на экстремум функцию ![]()
![]() .
.
Решение. Частные производные ![]() обращаются в нуль в точках
обращаются в нуль в точках ![]() и
и ![]() . Других подозрительных на экстремум точек нет.
. Других подозрительных на экстремум точек нет.
Найдем вторые производные ![]() . В точке
. В точке ![]() имеем
имеем ![]() , следовательно, в этой точке нет экстремума. В точке
, следовательно, в этой точке нет экстремума. В точке ![]()
![]() , причем
, причем ![]() , следовательно, в точке
, следовательно, в точке ![]() функция имеет минимум
функция имеет минимум ![]() .
.
Пример 2. Исследовать на экстремум функцию ![]()
![]() .
.
Решение. Решая систему  найдем единственную стационарную точку
найдем единственную стационарную точку ![]() . Других критических точек нет. Находим вторые частные производные
. Других критических точек нет. Находим вторые частные производные ![]()
![]() . В точке
. В точке ![]() экстремум есть, так как
экстремум есть, так как ![]() , а поскольку
, а поскольку ![]() во всех точках, в том числе и в точке
во всех точках, в том числе и в точке ![]() , то в этой точке максимум:
, то в этой точке максимум: ![]() .
.
Пусть требуется найти наибольшее и наименьшее значения функции ![]() в замкнутой области
в замкнутой области ![]() . Эти значения функция может принимать в точках экстремума и на границе области
. Эти значения функция может принимать в точках экстремума и на границе области ![]() . Поэтому нужно найти значения функции в точках, подозрительных на экстремум, и значения на границе
. Поэтому нужно найти значения функции в точках, подозрительных на экстремум, и значения на границе ![]() , при этом нужно использовать уравнение границы, что позволяет свести задачу к нахождению наибольшего и наименьшего значения функции одной переменной на отрезке.
, при этом нужно использовать уравнение границы, что позволяет свести задачу к нахождению наибольшего и наименьшего значения функции одной переменной на отрезке.
Пример 3. Найти наименьшее и наибольшее значения ![]() в круге
в круге ![]() .
.
Решение. Находим стационарные точки из системы  . Получим единственную стационарную точку
. Получим единственную стационарную точку ![]() , сосчитаем
, сосчитаем ![]() . Исследуем поведение функции на границе: выражая
. Исследуем поведение функции на границе: выражая ![]() из уравнения границы
из уравнения границы ![]() и подставляя в формулу
и подставляя в формулу ![]() , получим функцию одной переменной
, получим функцию одной переменной ![]() . Найдем наименьшее и наибольшее значения полученной функции на отрезке
. Найдем наименьшее и наибольшее значения полученной функции на отрезке ![]() , для чего находим критические точки из условия
, для чего находим критические точки из условия ![]() , и считаем значения
, и считаем значения ![]() ,
, ![]() ,
, ![]() . Сравнивая полученные значения, видим, что наибольшее и наименьшее значения достигаются на границе области:
. Сравнивая полученные значения, видим, что наибольшее и наименьшее значения достигаются на границе области: ![]() в точках
в точках ![]() и
и ![]() ,
, ![]() в точках
в точках ![]() .
.
 Пример 4. Найти наибольшее и наименьшее значения функции
Пример 4. Найти наибольшее и наименьшее значения функции ![]() в замкнутой области, ограниченной кривыми
в замкнутой области, ограниченной кривыми 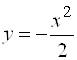 и
и ![]() .
.
Решение. Решая систему  найдем две стационарные точки
найдем две стационарные точки ![]() и
и ![]() , однако указанной области принадлежит только точка
, однако указанной области принадлежит только точка ![]() , поэтому находим
, поэтому находим ![]() . Теперь исследуем поведение функции на границе. В отличие от предыдущего примера, граница области состоит не из одной линии, а из двух кривых, заданных разными уравнениями, поэтому нужно отдельно провести исследование на каждой из частей.
. Теперь исследуем поведение функции на границе. В отличие от предыдущего примера, граница области состоит не из одной линии, а из двух кривых, заданных разными уравнениями, поэтому нужно отдельно провести исследование на каждой из частей.
На дуге параболы  ,
, ![]() функция
функция ![]() будет зависеть только от одной переменной:
будет зависеть только от одной переменной: ![]() . Найдем ее наименьшее и наибольшее значения на отрезке
. Найдем ее наименьшее и наибольшее значения на отрезке ![]() . Для этого, как обычно, найдем критические точки
. Для этого, как обычно, найдем критические точки 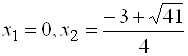 (точка
(точка  отброшена, так как она не принадлежит отрезку
отброшена, так как она не принадлежит отрезку ![]() ) и сосчитаем значение функции в этих точках и на границе:
) и сосчитаем значение функции в этих точках и на границе:
 .
.
На прямой ![]()
![]() тоже является функцией только от
тоже является функцией только от ![]() :
: ![]() ,
, ![]() . Найдем
. Найдем ![]() , откуда
, откуда ![]() и
и ![]() .
.
Значения в граничных точках уже найдены при исследовании границы  . Сравнивая полученные результаты, находим, что
. Сравнивая полученные результаты, находим, что
![]() , а
, а ![]() .
.
Задачи для самостоятельной работы.
1. Найдите ![]() и
и ![]() для функции
для функции  в точке
в точке ![]() .
.
Ответ: ![]() .
.
2. Найдите полный дифференциал функции ![]() .
.
Ответ:  .
.
3. Для функции ![]() найдите
найдите ![]() .
.
Ответ: 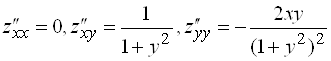 .
.
4. Найдите  для функции
для функции ![]() .
.
Ответ: 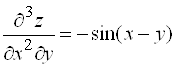 .
.
5. Для функции ![]() найдите
найдите ![]() .
.
Ответ: ![]() .
.
6. Дана функция  , где
, где ![]() ,
, ![]() . Найти
. Найти ![]() .
.
Ответ:  .
.
7. Дана функция 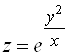 , где
, где ![]() ,
, ![]() . Найти
. Найти ![]() и
и ![]() .
.
Ответ: 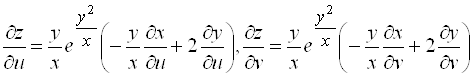 .
.
8. Исследовать на экстремум функцию ![]() .
.
Ответ:  , в точках
, в точках ![]() нет экстремума.
нет экстремума.
9. Найти наибольшее и наименьшее значения функции  в области
в области  .
.
Ответ: ![]() на всей границе.
на всей границе.
| < Предыдущая | Следующая > |
|---|