5.11.5 Частные производные и дифференциалы высших порядков
Частные производные функции нескольких переменных сами являются функциями этих переменных и могут иметь частные производные, которые для исходной функции будут частными производными второго порядка. Так, для функции ![]() можно определить четыре частные производные второго порядка, которые обозначаются символами
можно определить четыре частные производные второго порядка, которые обозначаются символами
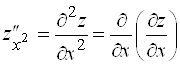 ,
, 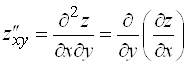 ,
,
 ,
, 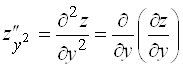 .
.
Частные производные ![]() и
и ![]() , отличающиеся порядком дифференцирования, называются смешанными частными производными второго порядка.
, отличающиеся порядком дифференцирования, называются смешанными частными производными второго порядка.
Пример 1. Найти частные производные второго порядка функции ![]() .
.
Решение. ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Пример 2. Найти частные производные второго порядка функции ![]() .
.
Решение. ![]() ;
;  ;
;
![]() ;
; 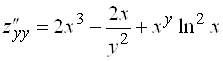 ;
;
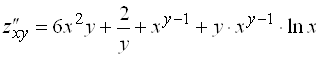 ;
; 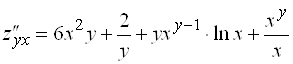 .
.
Можно определить производные еще более высоких порядков. Так, для функции ![]() можно написать восемь частных производных третьего порядка:
можно написать восемь частных производных третьего порядка: ![]() .
.
Аналогично определяются частные производные высших порядков для функции с любым числом независимых переменных.
В примерах 1 и 2 смешанные частные производные совпали, то есть ![]() , однако это не всегда так. Существуют различные условия, достаточные для того, чтобы величина смешанных частных производных не зависела от порядка дифференцирования. Приведем наиболее простое и часто употребляемое условие.
, однако это не всегда так. Существуют различные условия, достаточные для того, чтобы величина смешанных частных производных не зависела от порядка дифференцирования. Приведем наиболее простое и часто употребляемое условие.
Теорема 1. Если частные производные функции ![]() до
до ![]() порядка включительно непрерывны, то ее смешанные производные до
порядка включительно непрерывны, то ее смешанные производные до ![]() порядка не зависят от порядка дифференцирования.
порядка не зависят от порядка дифференцирования.
В рассмотренных выше примерах условия теоремы были выполнены, поэтому смешанные частные производные совпали.
Пусть ![]() и
и ![]() – независимые переменные. Дифференциалом второго порядка от функции
– независимые переменные. Дифференциалом второго порядка от функции ![]() называется дифференциал от полного дифференциала:
называется дифференциал от полного дифференциала: ![]() . Аналогично
. Аналогично ![]() . Дифференциалы высших порядков вычисляются в предположении, что
. Дифференциалы высших порядков вычисляются в предположении, что ![]() и
и ![]() остаются постоянными. Если
остаются постоянными. Если ![]() удовлетворяет условиям теоремы 1, то есть
удовлетворяет условиям теоремы 1, то есть ![]() , то формулу для вычисления
, то формулу для вычисления ![]() можно записать в виде:
можно записать в виде:
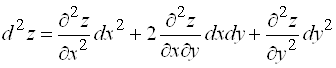 . (1)
. (1)
Это выражение напоминает формулу для квадрата суммы двух слагаемых. Выражение для ![]() напоминает формулу куба суммы двух слагаемых и имеет вид:
напоминает формулу куба суммы двух слагаемых и имеет вид:
 . (2)
. (2)
Эта аналогия в формулах может быть продолжена и дальше:
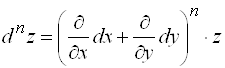 .
.
Дифференциалы высших порядков, начиная со второго, свойством инвариантности формы не обладают и выражения для них более громоздкие, чем формулы (1) и (2). Например, для функции ![]() , где
, где ![]() ,
, ![]() , второй дифференциал находится по формуле:
, второй дифференциал находится по формуле:
 .
.
Пример 3. Найти ![]() для функции
для функции 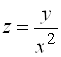 .
.
Решение. Находим
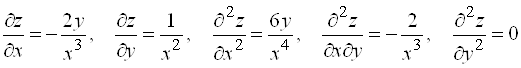 .
.
Теперь по формуле (1) находим 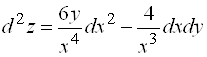 .
.
| < Предыдущая | Следующая > |
|---|