5.11.4 Производные сложной функции
При построении сложных функций нескольких переменных в качестве составляющих функций можно брать функции с различным числом независимых переменных. Запись в одной формуле всех возможных случаев громоздка. Поэтому ограничимся рассмотрением только нескольких случаев.
I. Пусть ![]() , где
, где ![]() ,
, ![]() . Тогда в конечном итоге
. Тогда в конечном итоге ![]() будет функцией одной переменной
будет функцией одной переменной ![]() :
: ![]() . Если существуют непрерывные частные производные
. Если существуют непрерывные частные производные ![]() и
и ![]() и существуют
и существуют ![]() и
и ![]() , то существует
, то существует ![]() , которая вычисляется по формуле:
, которая вычисляется по формуле:
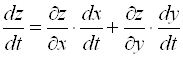 . (1)
. (1)
(Обращайте внимание на то, когда пишется круглое ![]() в обозначениях производных и когда прямое
в обозначениях производных и когда прямое ![]() .)
.)
В частности, если роль независимой переменной играет ![]() , то есть
, то есть ![]() , где
, где ![]() , то по формуле (1) получим:
, то по формуле (1) получим:
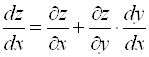 . (2)
. (2)
Здесь ![]() – частная производная по
– частная производная по ![]() функции двух аргументов
функции двух аргументов ![]() , а
, а ![]() – обычная производная функции
– обычная производная функции ![]() одной переменной.
одной переменной.
Производную ![]() в формуле (2) называют полной производной.
в формуле (2) называют полной производной.
Пример 1. Дана функция ![]() , где
, где ![]() . Найти
. Найти ![]() .
.
Решение. Находим производные (следите за обозначениями): 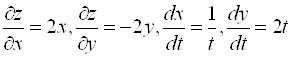 .
.
Теперь по формуле (1) находим: 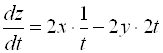 . Здесь можно заменить
. Здесь можно заменить ![]() и
и ![]() их выражениями через
их выражениями через ![]() :
: 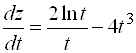 .
.
Искомую производную можно было найти и не применяя формулу (1). Для этого достаточно выразить ![]() через
через ![]() :
: ![]() и взять производную по
и взять производную по ![]() :
: 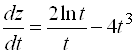 . Однако не следует делать вывода о ненужности формул дифференцирования сложной функции. Часто приходится искать производные, когда зависимость
. Однако не следует делать вывода о ненужности формул дифференцирования сложной функции. Часто приходится искать производные, когда зависимость ![]() от
от ![]() и
и ![]() или зависимость
или зависимость ![]() и
и ![]() от
от ![]() неизвестны, что не дает возможности явно выразить
неизвестны, что не дает возможности явно выразить ![]() через
через ![]() .
.
Пример 2. Дана функция ![]() , где
, где ![]() . Найти
. Найти ![]()
Решение. Функция ![]() зависит от
зависит от ![]() через посредство
через посредство ![]() и
и ![]() и явно выразить
и явно выразить ![]() через
через ![]() невозможно, поэтому здесь не удастся миновать формулы (1). Найдем
невозможно, поэтому здесь не удастся миновать формулы (1). Найдем  и применяем формулу (1):
и применяем формулу (1):  .
.
Пример 3. Дана функция ![]() , где
, где ![]() . Найти
. Найти ![]() .
.
Решение.
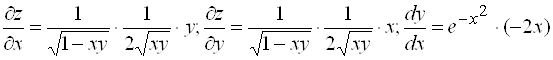 .
.
По формуле (2) получаем:
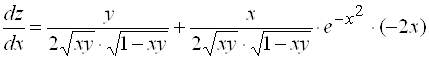 .
.
II. Пусть теперь ![]() , где
, где ![]() и существуют
и существуют 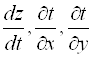 , тогда
, тогда ![]() через посредство
через посредство ![]() зависит от двух переменных
зависит от двух переменных ![]() и
и ![]() , то есть
, то есть ![]() и можно говорить о частных производных
и можно говорить о частных производных ![]() и
и ![]() , которые находятся по формулам:
, которые находятся по формулам: 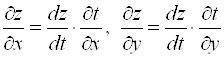 (обратите внимание на обозначения производных).
(обратите внимание на обозначения производных).
Пример 4. Пусть ![]() , где
, где ![]() . Тогда
. Тогда  является сложной функцией от
является сложной функцией от ![]() и от
и от ![]() . По последним формулам находим:
. По последним формулам находим:  .
.
III. Пусть ![]() и
и ![]() ,
, ![]() , тогда
, тогда ![]() является сложной функцией от
является сложной функцией от ![]() и
и ![]() :
: ![]() . Если существуют непрерывные частные производные
. Если существуют непрерывные частные производные ![]() и
и ![]() и существуют
и существуют 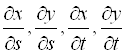 , то существуют
, то существуют ![]() и
и ![]() , которые вычисляются по формулам:
, которые вычисляются по формулам:
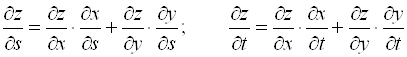 . (3)
. (3)
Пример 5. Пусть 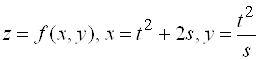 . Найти
. Найти 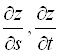 .
.
Решение. Найдем 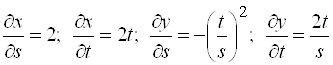 .
.
По формуле (3) получим:
 . (4)
. (4)
Если ![]() задана конкретной формулой, например
задана конкретной формулой, например ![]() , то можно найти:
, то можно найти:
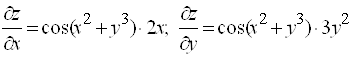 и подставить в (4):
и подставить в (4):

| < Предыдущая | Следующая > |
|---|