5.11.3 Частные производные. Полный дифференциал

Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных в точке частные производные определяются так:

,

,

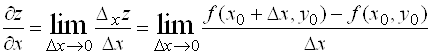Если эти пределы существуют.

Величина

Называется частным приращением функции в точке по аргументу (по аргументу ).

Используются и другие обозначения частных производных:

.

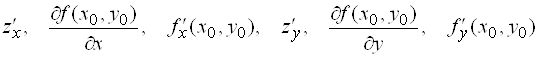Символы как дроби трактовать нельзя (в отличие от случая одной переменной). Правила вычисления частных производных остаются теми же, что и для функций одной переменной.

Пример 1. Найти частные производные функции .

Решение. При нахождении считаем постоянной и дифференцируем по , пользуясь правилом дифференцирования суммы и степенной функции: .

При отыскании считаем постоянной и дифференцируем по , пользуясь правилом дифференцирования суммы, степенной, логарифмической и показательной функций:

.

Пример 2. Найти частные производные функции:

.

Решение. Рассуждая как в предыдущем примере, получим:

.

Пример 3. Пусть . Требуется найти ее частные производные.

Решение. Относительно аргумента функция является степенной, поэтому .

При нахождении и считаем постоянными, то есть относительно является показательной функцией, поэтому .

Рассуждая аналогично, находим .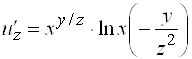

Пример 4. Найти частные производные функции .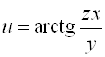

Решение. .

Ранее (в пункте 5.11.2.) полным приращением функции в точке назвали разность . Если полное приращение можно представить в виде

, (1)

Где и не зависят от и , а и стремятся к нулю при и , то функция называется дифференцируемой в точке , а линейная часть приращения функции (то есть та часть , которая зависит от и линейно) называется полным дифференциалом (или просто дифференциалом) этой функции в точке и обозначается символом :

. (2)

Если функция дифференцируема в точке, то она непрерывна в ней, так как при и . Из дифференцируемости функции в точке следует существование ее частных производных в этой точке. Действительно, полагая в (1) , имеем:

(частное приращения по ).

Деля на и переходя к пределу при , получаем , то есть .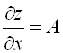

Аналогично, . Тогда выражение (2) можно переписать в виде .

Полагают тогда

. (3)

Обращаем внимание на то, что одного только существования частных производных в точке недостаточно для дифференцируемости функции в этой точке. Надо еще потребовать выполнения дополнительного условия – эти производные должны быть непрерывны в этой точке (сравните с функцией одного переменного).

Дифференциал функции двух переменных обладает свойством инвариантности его формы, как и дифференциал функции одной переменной.

Пример 5. Найти полный дифференциал следующих функций:

1) , 2) .

Решение.

1) Найдем частные производные:

и

.

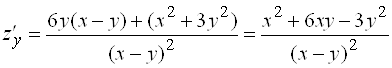Тогда по формуле (3):

.

2) и .

< Предыдущая		Следующая >