5.11.2 Предел и непрерывность функции двух переменных
Определение. Число ![]() называется пределом функции
называется пределом функции ![]() в точке
в точке ![]() , если
, если ![]() такое, что для тех пар чисел
такое, что для тех пар чисел ![]() (из области определения и отличных от
(из области определения и отличных от ![]() ), которые удовлетворяют неравенствам
), которые удовлетворяют неравенствам ![]() , выполняется неравенство
, выполняется неравенство ![]() .
.
Обозначают это так:  .
.
Все положения теории пределов функции одной переменной легко переносятся без существенных изменений на функции нескольких переменных.
Определение. Пусть ![]() определена в точке
определена в точке ![]() и в некоторой ее окрестности. Если
и в некоторой ее окрестности. Если 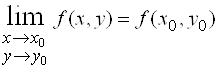 , то функция
, то функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() .
.
Подчеркнем, что предел не зависит от того, каким образом точка ![]() стремится к точке
стремится к точке ![]() .
.
Обозначим ![]() . Полным приращением функции
. Полным приращением функции ![]() при переходе от точки
при переходе от точки ![]() к точке
к точке ![]() называется разность
называется разность ![]() , то есть
, то есть ![]() . Для непрерывной функции
. Для непрерывной функции ![]() при
при ![]() .
.
Очевидно, что из непрерывности функции двух переменных в точке ![]() следует непрерывность функции одной переменной
следует непрерывность функции одной переменной ![]() при
при ![]() и
и ![]() при
при ![]() . Обратное утверждение, вообще говоря, неверно.
. Обратное утверждение, вообще говоря, неверно.
Если в какой-либо точке плоскости для ![]() нарушается условие
нарушается условие 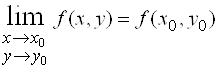 , то функция имеет разрыв в этой точке.
, то функция имеет разрыв в этой точке.
Пример 3. Найти пределы, если они существуют:
1) 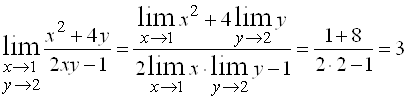 .
.
2)  . Положим
. Положим ![]() , тогда
, тогда
 .
.
3)  . Так как предел не должен зависеть от способа стремления к точке
. Так как предел не должен зависеть от способа стремления к точке ![]() , то пусть
, то пусть ![]() (
(![]() при
при ![]() ), тогда
), тогда 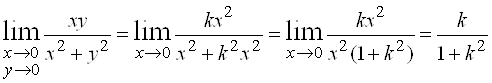 , то есть при разных
, то есть при разных ![]() будем получать разные ответы, следовательно, данная функция в точке
будем получать разные ответы, следовательно, данная функция в точке ![]() предела не имеет.
предела не имеет.
4)  . Будем стремиться к точке
. Будем стремиться к точке ![]() по прямым
по прямым ![]() , тогда
, тогда 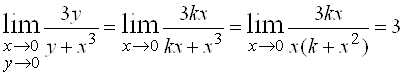 .
.
А теперь устремимся к началу координат по кривой ![]() :
:
 , то есть предел функции зависит от способа стремления к предельной точке. Иначе: функция имеет два предела в одной точке, чего быть не может. Следовательно, функция
, то есть предел функции зависит от способа стремления к предельной точке. Иначе: функция имеет два предела в одной точке, чего быть не может. Следовательно, функция 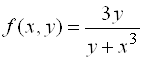 не имеет предела в точке
не имеет предела в точке ![]() .
.
Пример 4. Исследовать на непрерывность функции:
1)  ; 2)
; 2)  ; 3)
; 3) ![]() .
.
Решение. 1) Числитель и знаменатель функции ![]() являются непрерывными функциями на всей плоскости, дробь будет непрерывна всюду, кроме точек, в которых знаменатель равен нулю, то есть исключая начало координат.
являются непрерывными функциями на всей плоскости, дробь будет непрерывна всюду, кроме точек, в которых знаменатель равен нулю, то есть исключая начало координат.
2) Рассуждая аналогично, придем к выводу, что функция ![]() непрерывна всюду, кроме точек прямой
непрерывна всюду, кроме точек прямой ![]() .
.
3) Поскольку ![]() непрерывная функция на всей плоскости, а тангенс непрерывен при всех конечных значениях аргумента, кроме точек
непрерывная функция на всей плоскости, а тангенс непрерывен при всех конечных значениях аргумента, кроме точек ![]() , то функция
, то функция ![]() терпит разрыв там, где
терпит разрыв там, где ![]() .
.
Задачи для самостоятельного решения.
1. Найти следующие пределы:
А)  . Ответ: 165.
. Ответ: 165.
Б) 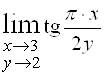 . Ответ:
. Ответ: ![]() .
.
В)  . Ответ:
. Ответ: ![]() .
.
2. Покажите, что функция  не имеет предела в точке
не имеет предела в точке ![]() .
.
3. Проверьте, везде ли непрерывны данные функции и если нет, то укажите, где расположены их точки разрыва:
А) ![]() . Ответ: непрерывна всюду.
. Ответ: непрерывна всюду.
Б) 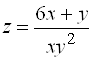 . Ответ: разрывы на прямых
. Ответ: разрывы на прямых ![]() и
и ![]() .
.
В) 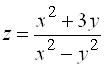 . Ответ: разрывы на биссектрисах координатных углов
. Ответ: разрывы на биссектрисах координатных углов ![]() .
.
Г) ![]() . Ответ: разрывы на прямой
. Ответ: разрывы на прямой ![]() .
.
| < Предыдущая | Следующая > |
|---|