5.10.12 Общая схема исследования функций и построение графиков

Существует способ построения графика функции, основанный на аналитическом исследовании функции. Исследование проводится по следующей примерной схеме:

1) выяснение области определения функции;

2) решается вопрос о четности или нечетности функции;

3) исследуется периодичность функции;

4) находят точки пересечения кривой с осями координат;

5) находят точки разрыва функции и определяют их характер;

6) проводят исследования на экстремум, находят экстремальные значения функции;

7) ищутся точки перегиба и интервалы выпуклости и вогнутости кривой;

8) отыскание асимптот кривой;

9) полученные результаты наносят на чертеж и получают график исследуемой функции.

Пример. Провести полное исследование функции 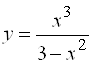и построить ее график.

Решение.

1) Функция определена всюду, кроме точек .

2) Функция нечетная, так как , и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для .

3) Функция не периодическая.

4) Так как только при , то пересечение с осями координат происходит только в начале координат.

5) Функция имеет разрыв второго рода в точке , причем , 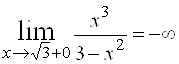. Попутно отметим, что прямая – вертикальная асимптота.

6) Находим и приравниваем ее к нулю: , откуда . На экстремум надо исследовать только точку (точку не исследуем, так как она является граничной точкой промежутка ).

В окрестности точки имеет: при и при , следовательно, в точке функция имеет максимум, .

7) Находим . Видим, что только при , при этом при и при , следовательно, в точке кривая имеет перегиб. Иногда направление вогнутости может измениться при переходе через разрыв кривой, поэтому следует выяснить знак и около точек разрыва функции. В нашем случае на промежутке и на , следовательно, на кривая вогнута и выпукла на .

8) Выясним вопрос об асимптотах.

Наличие вертикальной асимптоты установлено выше. Ищем горизонтальные: 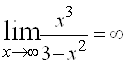, следовательно, горизонтальных асимптот нет.

Найдем наклонные асимптоты: , , следовательно, – наклонная двусторонняя асимптота.

9) Теперь, используя полученные данные, строим чертеж:

5.11 Дифференциальное исчисление функций нескольких переменных

В разделе 5.10 мы намеренно ограничились изучением только функций одной переменной, так как математическая теория в этом случае является наиболее простой. Теперь перенесем основные идеи и методы дифференциального исчисления на более общие случаи – функции нескольких переменных.

Читателю настоятельно рекомендуется сравнивать каждое новое вводимое понятие с уже известными аналогичными понятиями для функций одной переменной и отмечать, какие изменения в этих основных понятиях вызываются увеличением числа переменных.

В этом разделе рассматриваются функции двух переменных. Распространение определений и теорем на функции трех и более переменных представляет собой, как правило, лишь технические трудности.

< Предыдущая		Следующая >