5.10.11 Асимптоты кривой
Понятие асимптот вводится для кривых, график которых (или отдельные ветви графика) уходит в бесконечность. Это может быть, когда функция не ограничена или когда она задана на неограниченном промежутке.
Определение. Прямая линия называется асимптотой кривой ![]() , если расстояние точки кривой до этой прямой стремится к нулю при стремлении точки к бесконечности.
, если расстояние точки кривой до этой прямой стремится к нулю при стремлении точки к бесконечности.
Пример 1. Доказать, пользуясь определением асимптоты, что прямая ![]() является асимптотой кривой
является асимптотой кривой 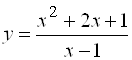 .
.
Решение. По определению асимптоты ![]() . В нашем случае
. В нашем случае  .
.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты.
Уравнение любой вертикальной прямой, то есть прямой, параллельной оси ![]() , имеет вид
, имеет вид ![]() .
.
 Если прямая
Если прямая ![]() является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции ![]() , то очевидно, что хотя бы один из односторонних пределов
, то очевидно, что хотя бы один из односторонних пределов ![]() или
или ![]() равен бесконечности (
равен бесконечности (![]() или
или ![]() ).
).
Все функции с бесконечными разрывами (разрывы второго рода) имеют вертикальные асимптоты.
Пример 2. Найти уравнение вертикальных асимптот графика функции 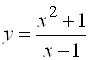 .
.
Решение. Видим, что ![]() , если
, если ![]() , точнее
, точнее  , то есть прямая
, то есть прямая ![]() является вертикальной асимптотой, причем двусторонней.
является вертикальной асимптотой, причем двусторонней.
Горизонтальные асимптоты.
 Всякая горизонтальная прямая имеет уравнение
Всякая горизонтальная прямая имеет уравнение ![]() .
.
Если прямая ![]() является горизонтальной асимптотой кривой
является горизонтальной асимптотой кривой ![]() , то
, то ![]() .
.
Пример 3. Найти горизонтальные асимптоты кривой ![]() .
.
Решение. Найдем 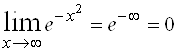 , то есть
, то есть ![]() при
при ![]() и при
и при ![]() , значит прямая
, значит прямая ![]() – горизонтальная асимптота данной кривой.
– горизонтальная асимптота данной кривой.
Наклонные асимптоты.
Уравнения наклонных асимптот обычно ищут в виде ![]() . По определению асимптоты
. По определению асимптоты ![]() или
или
![]() . (1)
. (1)
Разделим обе части этого равенства на ![]() :
:
 , откуда
, откуда
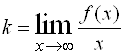 . (2)
. (2)
Теперь из (1):
![]() . (3)
. (3)
Для существования наклонных асимптот необходимо существование пределов (2) и (3). Если хотя бы один из них не существует, то наклонных асимптот нет. Пределы (2) и (3) нужно находить отдельно при ![]() и при
и при ![]() , так как пределы могут быть разными (функция имеет две разные асимптоты).
, так как пределы могут быть разными (функция имеет две разные асимптоты).
Пример 4. Найти наклонные асимптоты графика функции 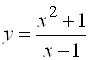 .
.
Решение. По формуле (2) найдем  .
.
Теперь найдем 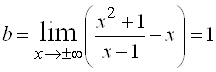 . Получаем уравнение наклонной асимптоты
. Получаем уравнение наклонной асимптоты ![]() .
.
Пример 5. Найти асимптоты кривой ![]() .
.
Решение. Вертикальных и горизонтальных асимптот нет, так как ![]() при
при ![]() . Ищем наклонные:
. Ищем наклонные:
 .
.
Таким образом, кривая асимптот не имеет.
Пример 6. Найти асимптоты кривой  .
.
Решение. Поскольку ![]() при
при ![]() и при
и при ![]() , то прямые
, то прямые ![]() и
и ![]() являются вертикальными асимптотами. Так как
являются вертикальными асимптотами. Так как  , то
, то ![]() – горизонтальная асимптота. Выясним вопрос о существовании наклонных асимптот:
– горизонтальная асимптота. Выясним вопрос о существовании наклонных асимптот: 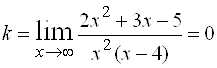 , следовательно, кривая наклонных асимптот не имеет (искать
, следовательно, кривая наклонных асимптот не имеет (искать ![]() не имеет смысла, так как горизонтальные асимптоты уже найдены).
не имеет смысла, так как горизонтальные асимптоты уже найдены).
Для самостоятельной работы.
1. Пользуясь определением асимптот, доказать, что прямая ![]() является асимптотой кривой
является асимптотой кривой  .
.
2. Найти асимптоты следующих кривых:
А)  . Ответ:
. Ответ: ![]() .
.
Б) 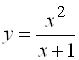 . Ответ:
. Ответ: ![]() .
.
В) ![]() . Ответ:
. Ответ: ![]() .
.
Г) ![]() . Ответ:
. Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|