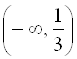5.10.10 Выпуклость и вогнутость графика функции. Точки перегиба
Определение. Пусть ![]() имеет в точке
имеет в точке ![]() конечную производную. Говорят, что кривая в точке
конечную производную. Говорят, что кривая в точке ![]() выпукла (вогнута), если в некоторой окрестности этой точки она лежит ниже (выше) касательной. Точку
выпукла (вогнута), если в некоторой окрестности этой точки она лежит ниже (выше) касательной. Точку ![]() называют точкой перегиба, если кривая переходит в точке
называют точкой перегиба, если кривая переходит в точке ![]() с одной стороны касательной на другую.
с одной стороны касательной на другую.
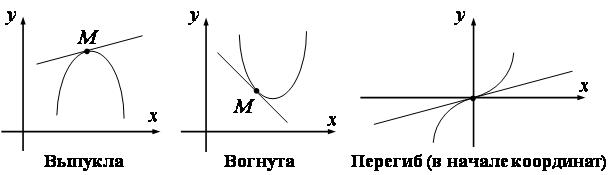 |
Определение. Если кривая выпукла (вогнута) в каждой точке некоторого промежутка, то она называется выпуклой (вогнутой) на этом промежутке.
Одна и та же кривая может состоять из выпуклых и вогнутых частей.
 Если будем, двигаясь по кривой в сторону возрастания
Если будем, двигаясь по кривой в сторону возрастания ![]() , следить за изменением угла
, следить за изменением угла ![]() , образованного касательной с положительным направ-лением
, образованного касательной с положительным направ-лением ![]() , то увидим, что на участках выпуклости этот угол уменьшается, а на участках вогнутости увеличивается. Так как с уменьшением
, то увидим, что на участках выпуклости этот угол уменьшается, а на участках вогнутости увеличивается. Так как с уменьшением ![]() ,
, ![]() уменьшается, а с увеличением
уменьшается, а с увеличением ![]() – увеличивается, то на участках выпуклости
– увеличивается, то на участках выпуклости ![]() убывает, следовательно,
убывает, следовательно, ![]() , а на участках вогнутости
, а на участках вогнутости ![]() возрастает, следовательно,
возрастает, следовательно, ![]() .
.
Итак, график будет выпуклым для тех интервалов оси ![]() , для которых
, для которых ![]() , и вогнут, где
, и вогнут, где ![]() . Точки перегиба – точки, при переходе через которые
. Точки перегиба – точки, при переходе через которые ![]() меняет знак. Отсюда получаем правило нахождения интервалов выпуклости, вогнутости и точек перегиба:
меняет знак. Отсюда получаем правило нахождения интервалов выпуклости, вогнутости и точек перегиба:
1) находим точки, в которых ![]() равна нулю, бесконечности или не существует;
равна нулю, бесконечности или не существует;
2) исследуем изменение знака ![]() при переходе через эти точки.
при переходе через эти точки.
Подчеркнем, что наличие равенства ![]() (необходимое условие перегиба) еще не обеспечивает наличие перегиба в точке
(необходимое условие перегиба) еще не обеспечивает наличие перегиба в точке ![]() . Например, для
. Например, для ![]() и
и ![]() , однако, легко убедиться, что кривая, изображающая эту функцию, в точке
, однако, легко убедиться, что кривая, изображающая эту функцию, в точке ![]() перегиба не имеет.
перегиба не имеет.
Пример 1. Найти интервалы выпуклости, вогнутости и точки перегиба кривой ![]() .
.
Решение. Находим производные ![]() ,
, 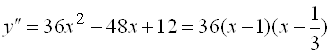 . Решая уравнение
. Решая уравнение ![]() , находим точки, подозрительные на перегиб:
, находим точки, подозрительные на перегиб:  . Область определения функции
. Область определения функции ![]() разбивается этими точками на три интервала
разбивается этими точками на три интервала  . На каждом из них
. На каждом из них ![]() будет постоянного знака, причем знаки по интервалам распределятся следующим образом:
будет постоянного знака, причем знаки по интервалам распределятся следующим образом:
|
|
|
|
|
|
|
|
|
– |
– |
+ | ||
|
|
– |
+ |
+ | ||
|
Знак |
+ |
– |
+ | ||
|
Вогнута |
Точка перегиба |
Выпукла |
Точка перегиба |
Вогнута |
Пример 2. Найти интервалы выпуклости, вогнутости и точки перегиба кривой ![]() .
.
Решение. Находим  . В данном случае
. В данном случае ![]() нигде в нуль не обращается, а в точке
нигде в нуль не обращается, а в точке ![]() она равна бесконечности, значит, в этой точке возможен перегиб. Так как при
она равна бесконечности, значит, в этой точке возможен перегиб. Так как при ![]() вторая производная
вторая производная ![]() и при
и при ![]() , то на
, то на ![]() кривая выпукла, а на
кривая выпукла, а на ![]() – вогнута и точка
– вогнута и точка ![]() – точка перегиба.
– точка перегиба.
Пример 3. Исследовать на перегиб кривую ![]() .
.
Решение. Функция определена при ![]() , то есть на
, то есть на ![]() . Найдем ее производные первого и второго порядков:
. Найдем ее производные первого и второго порядков:
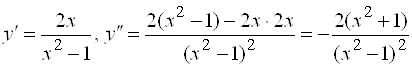 .
. ![]()
Так как при всех ![]() из области определения функции
из области определения функции ![]() , то кривая всюду выпукла и точек перегиба не имеет.
, то кривая всюду выпукла и точек перегиба не имеет.
Задачи для самостоятельного решения.
1. Найти точки перегиба и интервалы выпуклости и вогнутости следующих кривых:
A) ![]() .
.
Ответ: выпукла на ![]() ; вогнута на
; вогнута на ![]() ; точка перегиба
; точка перегиба ![]() .
.
Б) ![]() .
. ![]()
Ответ: точка перегиба ![]() ; выпукла на
; выпукла на ![]() и вогнута на
и вогнута на ![]() .
.
2. Показать, что кривая ![]() всюду вогнута.
всюду вогнута.
3. На примере функции ![]() убедиться, что между абсциссами точек перегиба кривой может и не быть точек экстремума.
убедиться, что между абсциссами точек перегиба кривой может и не быть точек экстремума.
| < Предыдущая | Следующая > |
|---|