5.10.06 Производные и дифференциалы высших порядков

Производная дифференцируемой функции , называемая производной первого порядка, представляет собой тоже функцию от , по отношению к которой можно ставить вопрос о ее производной.

Определение. Производная от производной первого порядка называется производной второго порядка или второй производной. Производная от второй производной называется производной третьего порядка или третьей производной и т. д.

Производные, начиная со второй, называются производными высших порядков и обозначаются: или

Производная -го порядка есть производная от производной -го порядка, то есть .

Пример 1. Найти производные до четвертого порядка включительно следующих функций:

Решение.

1) .

2) .

3) .

В некоторых случаях можно получить общий вид -й производной, по которому сразу записывается производная любого порядка (при этом предшествующие производные не вычисляются). Например, для функции имеем , следовательно . Для функций и можно показать, что .

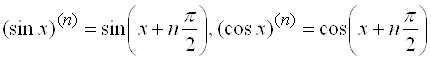Для отыскания производных высших порядков от произведения двух функций можно применять формулу Лейбница:

Пример 2. Найти для функции .

Решение. Обозначая , по формуле Лейбница получим .

В случае параметрического задания функции первую производную вычисляли по формуле:

(*)

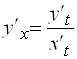И записывали тоже в параметрической форме:

К ней снова применим формулу (*) (при условии, что производные второго порядка существуют):

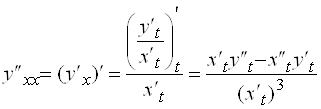Результат тоже записываем в параметрической форме и берем третью производную и т. д. Так можно получить производную от по любого порядка.

Пример 3. Найти функции

Решение. Найдем по формуле (*): .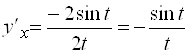

Производную запишем в параметрической форме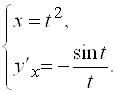

К этой функции снова применим формулу (*):

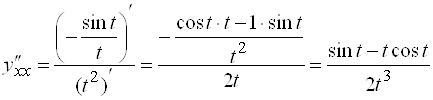Пример 4. Для функции найти .

Решение. 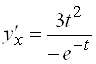тогда и 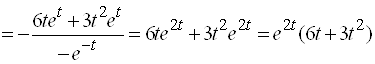. Получаем

Еще раз применяем формулу (*):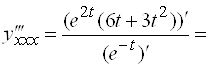

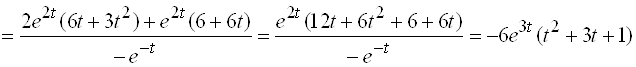Если требуется получить зависимость от , то выражаем из соотношения и подставляем в .

Для функций, заданных неявно, производные высших порядков можно находить тем же способом, что и первую производную, так как производная любого порядка сама является функцией, заданной неявно, если ее не разрешать относительно производной предыдущего порядка.

Пример 5. Дана функция . Найти .

Решение. Берем первую производную, считая функцией от : . Результат дифференцирования тоже функция, заданная неявно (если не разрешать ее относительно ). Дифференцируем ее, считая и функциями от :

Пример 6. Найти для функции .

Решение. . Не находя , дифференцируем полученное выражение еще раз как неявную функцию: . Полученное выражение снова рассматриваем как неявную функцию и берем от нее производную по : , или . Еще раз дифференцируя, найдем четвертую производную: .

Дифференциал от дифференциала функции называется дифференциалом второго порядка или вторым дифференциалом этой функции и обозначается через . Найдем выражение для :

Аналогично . Вообще дифференциалом -го порядка называется дифференциал от дифференциала -го порядка, то есть .

Дифференциалы высших порядков, начиная со второго, свойством инвариантности формы не обладают, то есть формула верна, когда – независимая переменная и перестает быть верной, когда – функция. Например, в случае дифференциал второго порядка вычисляется по формуле , где .

Пример 7. Найти и от функции в случаях, когда: 1) – независимая переменная, 2) – функция от другой независимой переменной.

Решение. Дифференциал первого порядка в силу свойства инвариантности его формы в обоих случаях представляется одинаково: .

В первом случае под понимается приращение независимой переменной , во втором – дифференциал от как от функции . Для отыскания приходится решать задачу для каждого случая отдельно.

1) Пусть – независимая переменная. Тогда, имея в виду, что в этом случае является постоянной величиной и ее можно выносить за знак дифференциала, получим:

2) Пусть теперь – функция от некоторой другой переменной. В этом случае уже не будет постоянной и выносить ее за знак дифференциала, как в первом случае, нельзя. Нужно вычислить дифференциал от как от произведения:

< Предыдущая		Следующая >