5.10.05 Дифференциал функции
Определение. Функция ![]() называется дифференцируемой в точке
называется дифференцируемой в точке ![]() , если ее приращение в этой точке можно представить в виде
, если ее приращение в этой точке можно представить в виде ![]() , где
, где ![]() – константа, а
– константа, а ![]() – бесконечно малая при
– бесконечно малая при ![]() .
.
Требование дифференцируемости функции в точке эквивалентно существованию производной в этой точке, причем ![]() .
.
Пусть ![]() дифференцируема в точке
дифференцируема в точке ![]() и
и ![]() , тогда
, тогда ![]() , где
, где ![]() при
при ![]() . Величина
. Величина ![]() и каждое слагаемое правой части являются бесконечно малыми величинами при
и каждое слагаемое правой части являются бесконечно малыми величинами при ![]() . Сравним их:
. Сравним их: 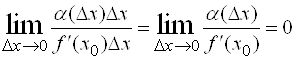 , то есть
, то есть ![]() – бесконечно малая более высокого порядка, чем
– бесконечно малая более высокого порядка, чем ![]() .
.
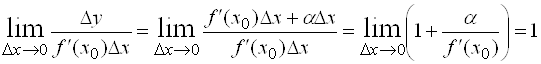 , то есть
, то есть ![]() . Следовательно,
. Следовательно, ![]() представляет собой главную и вместе с тем линейную относительно
представляет собой главную и вместе с тем линейную относительно ![]() часть приращения
часть приращения ![]() (линейная – значит содержащая
(линейная – значит содержащая ![]() в первой степени). Это слагаемое называют дифференциалом функции
в первой степени). Это слагаемое называют дифференциалом функции ![]() в точке
в точке ![]() и обозначают
и обозначают ![]() или
или ![]() . Итак, для произвольных значений
. Итак, для произвольных значений ![]()
![]() . (1)
. (1)
Полагают ![]() , тогда
, тогда
![]() . (2)
. (2)
Как видим, для нахождения дифференциала нужно умножить производную на ![]() . Это позволяет из таблицы формул для производных сразу записать соответствующую таблицу для дифференциалов. Например, умножив обе части формулы
. Это позволяет из таблицы формул для производных сразу записать соответствующую таблицу для дифференциалов. Например, умножив обе части формулы ![]() на
на ![]() , получим
, получим ![]() , или
, или ![]() .
.
Дифференциал функции ![]() линейно выражается через
линейно выражается через ![]() , в то время как приращение
, в то время как приращение ![]() находится в более сложной зависимости от
находится в более сложной зависимости от ![]() .
.
Пример 1. Для функции ![]() найти выражение для
найти выражение для ![]() и
и ![]() при некоторых значениях
при некоторых значениях ![]() и
и ![]() .
.
Решение. ![]()
![]() ;
; ![]() (взяли главную линейную относительно
(взяли главную линейную относительно ![]() часть
часть ![]() ). В данном случае
). В данном случае ![]() .
.
Таким образом, с одной стороны, вычисление дифференциала значительно проще, чем вычисление приращения, с другой стороны, ![]() и допускаемая при этом погрешность может быть сделана сколь угодно малой за счет уменьшения
и допускаемая при этом погрешность может быть сделана сколь угодно малой за счет уменьшения ![]() . Эти обстоятельства позволяют во многих случаях заменять
. Эти обстоятельства позволяют во многих случаях заменять ![]() величиной
величиной ![]() . Из приближенного равенства
. Из приближенного равенства ![]() , учитывая, что
, учитывая, что ![]() , а
, а ![]() , получим
, получим ![]() , где
, где ![]() .
.
Пример 2. Вычислить ![]() .
.
Решение. Взяв функцию ![]() , имеем:
, имеем: ![]() . Полагая
. Полагая ![]() (выбираем сами, чтобы корень извлекался),
(выбираем сами, чтобы корень извлекался), ![]() , получим
, получим  .
.
Пример 3. Вычислить значение функции ![]() в точке
в точке ![]() .
.
Решение. В качестве ![]() возьмем число 0, то есть
возьмем число 0, то есть ![]() , тогда
, тогда ![]() и
и ![]() . По таблице
. По таблице ![]() . Ошибка получилась незначительная.
. Ошибка получилась незначительная.
Отметим еще одно важное свойство дифференциала. Формула для нахождения дифференциала ![]() верна как в случае, когда
верна как в случае, когда ![]() – независимая переменная, так и в случае, когда
– независимая переменная, так и в случае, когда ![]() – функция от новой переменной
– функция от новой переменной ![]() . Это свойство дифференциала называется свойством инвариантности его формы. Например, для функции
. Это свойство дифференциала называется свойством инвариантности его формы. Например, для функции ![]() дифференциал запишется в виде
дифференциал запишется в виде  независимо от того, является ли
независимо от того, является ли ![]() независимой переменной или функцией. В случае, если
независимой переменной или функцией. В случае, если ![]() – функция и конкретно задана, например
– функция и конкретно задана, например ![]() , то вычисление
, то вычисление ![]() можно продолжить, для чего найдем
можно продолжить, для чего найдем ![]() и подставим в ранее полученное выражение для
и подставим в ранее полученное выражение для ![]() :
:
 .
.
Если вместо формулы (2) воспользовались бы неинвариантной формулой (1), то в случае, когда ![]() – функция, мы не могли бы подобным образом продолжить вычисление
– функция, мы не могли бы подобным образом продолжить вычисление ![]() , так как
, так как ![]() , вообще говоря, не совпадает с
, вообще говоря, не совпадает с ![]() .
.
Задачи для самоконтроля.
1. Найти дифференциалы следующих функций:
А) ![]() ; Ответ:
; Ответ: ![]() .
.
Б) 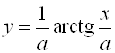 ; Ответ:
; Ответ:  .
.
В)  ; Ответ:
; Ответ:  .
.
2. Известно, что ![]() и
и ![]() – дифференцируемые функции от
– дифференцируемые функции от ![]() . Найти дифференциал функции
. Найти дифференциал функции ![]() , если:
, если:
А) ![]() ; Ответ:
; Ответ: ![]() .
.
Б)  ; Ответ:
; Ответ: 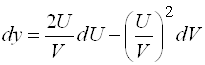 .
.
В) ![]() ; Ответ:
; Ответ: 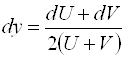 .
.
3. Найти приращение и дифференциал функции ![]() в точке
в точке ![]() при
при ![]() и
и ![]() . Найти для каждого из этих значений
. Найти для каждого из этих значений ![]() абсолютную
абсолютную ![]() и относительную
и относительную  погрешности, которые допускаются при замене приращения дифференциалом функции.
погрешности, которые допускаются при замене приращения дифференциалом функции.
Ответ: при ![]() , абсолютная погрешность 8, относительная
, абсолютная погрешность 8, относительная ![]() ; при
; при ![]() , абсолютная погрешность 0,062, относительная
, абсолютная погрешность 0,062, относительная ![]() ; при
; при ![]()
![]() , абсолютная погрешность 0,0006, относительная
, абсолютная погрешность 0,0006, относительная ![]() .
.
4. Вычислить приближенно:
А) ![]() при
при ![]() . Ответ:
. Ответ: ![]() .
.
Б) ![]() при
при ![]() . Ответ:
. Ответ: ![]() .
.
В) ![]() . Ответ:
. Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|