5.10.04 Дифференцирование функций, заданных параметрически и неявно

Зависимость функции от аргумента может осуществляться через посредство третьей переменной , называемой параметром:

.

В этом случае говорят, что функция от задана параметрически. Параметрическое задание функции удобно тем, что оно дает общую запись для прямой и обратной функций.

Предположим, что на некотором промежутке функции и имеют производные, причем . Кроме того, для существует обратная функция (производная обратной функции равна обратной величине производной прямой функции).

Тогда – сложная функция и ее производная: . Производную тоже запишем в параметрической форме:

Пример 1. Найти производную функции по , заданной параметрически:

Решение. 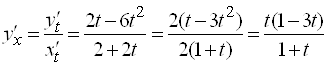. Запишем функцию в параметрической форме:

Пусть дано уравнение , не разрешенное относительно . Если существует такая, что , то говорят, что уравнение задает как функцию от неявно. Обычное задание функции называют явным.

При таком способе задания функции производную находим, дифференцируя уравнение , считая функцией от (по правилу дифференцирования сложной функции).

Пример 2. Найти производную , не решая уравнения: относительно .

Решение. Так как в правой части уравнения стоит нуль, а производная постоянной равна нулю, то .

Применяя почленное дифференцирование, найдем , откуда .

Пример 3. Найти функции, заданной неявно уравнением .

Решение. (производную от берем как производную сложной функции). Разрешая уравнение относительно (что не всегда возможно), найдем .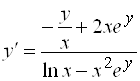

< Предыдущая		Следующая >