5.10.02 Правила дифференцирования и таблица производных
Для удобства нахождения производных различных функций запишем все правила и формулы дифференцирования в одну таблицу. Их нужно обязательно запомнить:
1) 
;
2) 
;
3) 
;
4) 
;
5) 
;
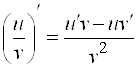6) 
;
7) 
;
8) 
;
9) 
;
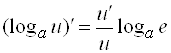10) 
;
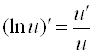11) 
;
12) 
;
13) 
;
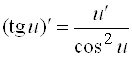14) 
;
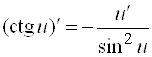15) 
;
16) 
;
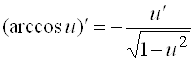17) 
;
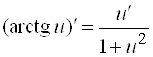18) 
;
19) 
;
20) 
;
21) 
;
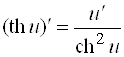22) 
.
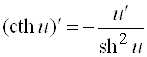Здесь 
и 
– дифференцируемые функции,
– синус гиперболический,
– гиперболический косинус,
– гиперболический тангенс,
– гиперболический котангенс.
Если 
(следовательно 
), то получим частный случай формул 6-22:
1) 
;
2) 
;
3) 
;
4) 
;
5) 
;
6) 
;
7) 
;
8) 
;
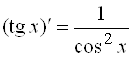9) 
;
10) 
;
11) 
;
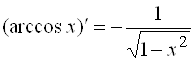12) 
;
13) 
;
14) 
;
15) 
;
16) 
;
17) 
.
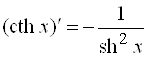Напомним также правило дифференцирования сложной функции: пусть дана сложная функция 
, где 
, и пусть в точке 
функция 
имеет 
, а 
имеет производную в точке 
, тогда 
имеет производную в точке , причем 
или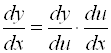 
.
Это правило распространяется на любое число промежуточных аргументов. Так, если 
, где 
, а 
и 
, то 
.
В практике дифференцирования не записывают сложную функцию в виде цепочки простейших элементарных функций, а держат ее (и правила дифференцирования) в памяти.
Пример 1. Найти производную от функции
.
Решение. Берем сначала производную от натурального логарифма, считая в качестве его аргумента все выражение, стоящее под знаком логарифма. Получим 
. Затем берем производную от синуса, у которого аргумент – все, что стоит после 
: 
. Выражение, стоящее под знаком синуса, есть квадратный корень некоторого выражения. Берем производную от корня: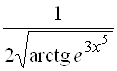 
. Теперь берем производную от подкоренного выражения, начиная с арктангенса: 
. Под знаком арктангенса стоит показательная функция – находим производную показательной функции: 
. И, наконец, находим производную от показателя по правилу дифференцирования степени: 
. Записав в виде произведения получившиеся результаты дифференцирования, получим выражение искомой производной:
.
Такой способ дифференцирования быстрее приводит к цели и не загромождает записи.
Для дифференцирования показательно–степенной функции 
, ее можно представить в виде 
и дифференцировать как сложную функцию от 
. В результате получим 
.
Таким образом, можно сформулировать следующее мнемоническое правило: чтобы найти производную показательно-степенной функции, достаточно продифференцировать ее как показательную (то есть предполагая основание постоянным), а затем как степенную (предполагая показатель постоянным) и полученные результаты сложить.
Пример 2. Найти производную функции 
.
Решение. Продифференцируем данную функцию, считая ее показательной, то есть полагая, что 
. Получим: 
. Теперь дифференцируем ее как степенную: 
. Для окончательного ответа осталось только сложить полученные результаты дифференцирования.
| < Предыдущая | Следующая > |
|---|
