5.10.01 Понятие производной, ее геометрический смысл

Определение. Производной функции в точке называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю, то есть

.

Если такого предела не существует, то говорят, что функция в точке производной не имеет. В случае, когда предел равен бесконечности определенного знака, говорят, что существует бесконечная производная.

Для обозначения производных пользуются символами: .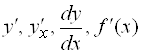

Функция, имеющая конечную производную в точке, называется дифференцируемой, а действие нахождения производной – дифференцированием. Способ вычисления производной следует из ее определения.

Пример 1. Пользуясь определением производной, найти производную функции в точке .

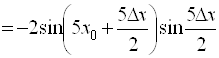Решение. Значению придадим приращение , тогда функция получит приращение . Составим отношение и перейдем в нем к пределу при :

.

Итак, .

Поскольку производная определяется через предел, можно говорить об односторонних производных, понимая под этим односторонний предел: 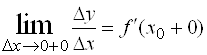или .

Если в точке существует обычная производная , то в ней есть односторонние производные, причем . Обратно, если существуют равные между собой и , то существует , равная их общему значению. Если , то в точке не существует обычной производной. На концах речь может идти только об односторонних производных.

Геометрический смысл производной функции в точке заключается в том, что равна тангенсу угла наклона к оси касательной к графику функции в точке

Учитывая геометрический смысл и коэффициента в уравнении прямой , можно записать уравнение касательной к графику функции в виде

,

А уравнение нормали в точке в виде

.

(Под нормалью к кривой в точке понимается прямая, проходящая через эту точку перпендикулярно касательной).

< Предыдущая		Следующая >