5.09.3 Примеры разрывных функций

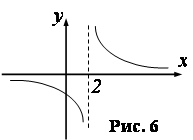Пример 1. Функция 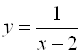определена и непрерывна на за исключением точки . Определим тип разрыва. Поскольку 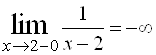и , то в точке разрыв второго рода (рис. 6).

Пример 2. Функция определена и непрерывна при всех , кроме , где знаменатель равен нулю. Найдем односторонние пределы в точке :

.

Односторонние пределы конечны и различны, следовательно, – точка разрыва первого рода (рис. 7).

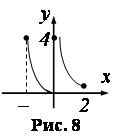Пример 3. Установить, в каких точках и какого рода разрывы имеет функция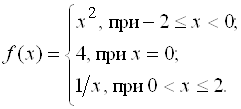

Эта функция определена на . Так как и непрерывны соответственно в промежутках и , то разрыв может быть только на стыке промежутков, то есть в точке . Поскольку 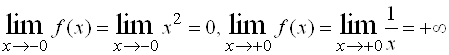, то является точкой разрыва второго рода.

Пример 4. Можно ли устранить разрывы функций:

А)  в точке ;

Б)  в точке ;

В)  в точке ?

Решение. О примере а) сразу можно сказать, что разрыв в точке устранить невозможно, так как в этой точке бесконечные односторонние пределы (см. пример 1).

Б) Функция хотя имеет конечные односторонние пределы в точке

(,),

Но они не совпадают, поэтому разрыв также устранить нельзя.

В) Функция в точке разрыва имеет равные односторонние конечные пределы: . Следовательно, разрыв может быть устранен переопределением функции в точке , если положить вместо .

Пример 5. Показать, что функция Дирихле

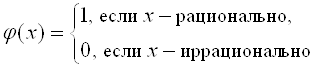
Разрывна в каждой точке числовой оси.

Решение. Пусть – любая точка из . В любой ее окрестности найдутся как рациональные, так и иррациональные точки. Значит, в любой окрестности функция будет иметь значения, равные 0 и 1. В таком случае не может существовать предела функции в точке ни слева, ни справа, значит функция Дирихле в каждой точке числовой оси имеет разрывы второго рода.

Пример 6. Найти точки разрыва функции

И определить их тип.

Решение. Точками, подозрительными на разрыв, являются точки .

В точке имеет разрыв второго рода, так как

.

Точка является точкой непрерывности, так как значение функции в этой точке и в ее окрестности определяется второй строкой, а не первой: .

Исследуем точку : , , откуда следует, что – точка разрыва первого рода.

Для самостоятельного решения.

Исследовать функции на непрерывность и определить тип точек разрыва:

1) ; Ответ: – точка устранимого разрыва;

2) ; Ответ: Разрыв второго рода в точке ;

3) 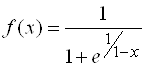; Ответ: Разрыв первого рода при ;

4)

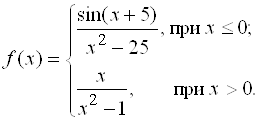
Ответ: В точке устранимый разрыв, в – разрыв второго рода и в точке - разрыв первого рода.

5) Как следует выбрать число , чтобы функция

Была бы непрерывной в точке ?

Ответ: .

6) Можно ли подобрать число так, чтобы функция

Была бы непрерывной в точке ?

Ответ: нет.

5.10 Дифференциальное исчисление функций одной переменной

В этом разделе центральное место занимают понятия производной и дифференциала. Кроме усвоения содержательной стороны излагаемых вопросов, этот раздел требует продолжительной работы по усвоению техники дифференцирования. Нужно довести свое умение дифференцировать до такой степени, чтобы дифференцирование элементарных функций любой сложности не вызывало затруднений. Для этого необходимо решить большое количество примеров. Помещенные здесь упражнения для самостоятельной работы нужно рассматривать лишь как небольшую часть всей работы. Рекомендуем еще обратиться за примерами к другим источникам.

< Предыдущая		Следующая >