5.09.2 Разрывы функции и их классификация

Признаком непрерывности функции в точке служит равенство 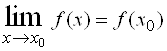, которое подразумевает наличие трех условий:

1) определена в точке ;

2) ;

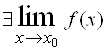3) .

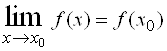Если хотя бы одно из этих требований нарушено, то называют точкой разрыва функции. Другими словами, точкой разрыва называется точка, в которой эта функция не является непрерывной. Из определения точек разрыва следует, что точками разрыва функции являются:

А) точки, принадлежащие области определения функции, в которых теряет свойство непрерывности,

Б) точки, не принадлежащие области определения , которые являются смежными точками двух промежутков области определения функции.

Например, для функции точка есть точка разрыва, так как функция в этой точке не определена, а функция 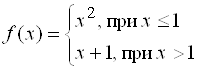имеет разрыв в точке , являющейся смежной для двух промежутков и области определения и не существует (см пункт 5.7.2).

Для точек разрыва принята следующая классификация.

1) Если в точке имеются конечные и , но , то называется Точкой разрыва первого рода, при этом называют Скачком функции.

Пример 2. Рассмотрим функцию

Разрыв функции возможен только в точке (в остальных точках она непрерывна как всякий многочлен).

Найдем , . Так как односторонние пределы конечны, но не равны друг другу, то в точке функция имеет разрыв первого рода. Заметим, что , следовательно функция в этой точке непрерывна справа (рис. 2).

2) Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен или не существует.

Пример 3. Функция непрерывна для всех значений , кроме . Найдем односторонние пределы: , , следовательно – точка разрыва второго рода (рис. 3).

3) Точка называется Точкой устранимого разрыва, если .

Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) значение функции в этой точке, положив 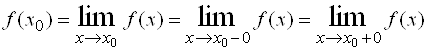, и функция станет непрерывной в точке .

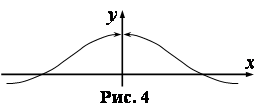Пример 4. Известно, что , причем этот предел не зависит от способа стремления к нулю. Но функция в точке не определена. Если доопределим функцию, положив , то она окажется непрерывной в этой точке (в остальных точках она непрерывна как частное непрерывных функций и ).

Пример 5. Исследовать на непрерывность функцию .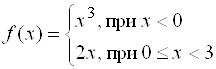

Решение. Функции и определены и непрерывны всюду, в том числе и в указанных промежутках. Исследуем точку стыка промежутков :

, , . Получаем, что , откуда следует, что в точке функция непрерывна.

Определение. Функция, непрерывная на промежутке за исключением конечного числа точек разрыва первого рода или устранимого разрыва, называется кусочно-непрерывной на этом промежутке.

< Предыдущая		Следующая >