5.09.1 Непрерывные функции. Основные понятия и свойства
Определение. Пусть на некотором промежутке определена функция ![]() и
и ![]() – точка этого промежутка. Если
– точка этого промежутка. Если 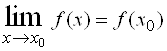 , то
, то ![]() называется непрерывной в точке
называется непрерывной в точке ![]() .
.
Из определения следует, что о непрерывности можно говорить лишь по отношению к тем точкам, в которых ![]() определена (при определении предела функции такого условия не ставилось). Для непрерывных функций
определена (при определении предела функции такого условия не ставилось). Для непрерывных функций  , то есть операции
, то есть операции ![]() и
и ![]() перестановочны. Соответственно двум определениям предела функции в точке можно дать два определения непрерывности – «на языке последовательностей» и «на языке неравенств» (на языке
перестановочны. Соответственно двум определениям предела функции в точке можно дать два определения непрерывности – «на языке последовательностей» и «на языке неравенств» (на языке ![]() ). Предлагается это сделать самостоятельно.
). Предлагается это сделать самостоятельно.
Для практического использования иногда более удобно определение непрерывности на языке приращений.
Величина ![]() называется приращением аргумента, а
называется приращением аргумента, а ![]() – приращением функции при переходе из точки
– приращением функции при переходе из точки ![]() в точку
в точку ![]() .
.
Определение. Пусть ![]() определена в точке
определена в точке ![]() . Функция
. Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть
, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть ![]() при
при ![]() .
.
Пример 1. Доказать, что функция ![]() непрерывна при любом значении
непрерывна при любом значении ![]() .
.
Решение. Пусть ![]() – произвольная точка. Придавая ей приращение
– произвольная точка. Придавая ей приращение ![]() , получим точку
, получим точку ![]() . Тогда
. Тогда ![]()
![]()
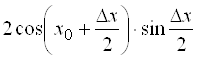 . Получаем
. Получаем ![]() .
.
Определение. Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() справа (слева), если
справа (слева), если
 .
.
Функция, непрерывная во внутренней точке, будет одновременно непрерывной справа и слева. Справедливо и обратное утверждение: если функция непрерывна в точке слева и справа, то она будет непрерывной в этой точке. Однако функция может быть непрерывной только с одной стороны. Например, для 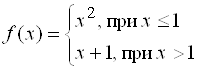
![]() ,
, ![]() ,
, ![]() , следовательно, эта функция непрерывна только слева (график этой функции см. выше в пункте 5.7.2).
, следовательно, эта функция непрерывна только слева (график этой функции см. выше в пункте 5.7.2).
Определение. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
В частности, если промежутком является отрезок ![]() , то на его концах подразумевается односторонняя непрерывность.
, то на его концах подразумевается односторонняя непрерывность.
Свойства непрерывных функций.
1. Все элементарные функции непрерывны в своей области определения.
2. Если ![]() и
и ![]() , заданные на некотором промежутке, непрерывны в точке
, заданные на некотором промежутке, непрерывны в точке ![]() этого промежутка, то в этой точке будут также непрерывны функции
этого промежутка, то в этой точке будут также непрерывны функции 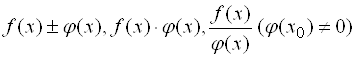 .
.
3. Если ![]() непрерывна в точке
непрерывна в точке ![]() из
из ![]() , а
, а ![]() непрерывна в соответствующей точке
непрерывна в соответствующей точке ![]() из
из ![]() , то и сложная функция
, то и сложная функция ![]() будет непрерывной в точке
будет непрерывной в точке ![]() .
.
| < Предыдущая | Следующая > |
|---|