5.08 Сравнение бесконечно малых и бесконечно больших
В процессе своего изменения одни бесконечно малые стремятся к нулю «быстрее», другие «медленнее». Например, 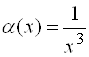 стремится к нулю при
стремится к нулю при ![]() «быстрее», чем
«быстрее», чем ![]() . Чтобы убедиться в этом, достаточно выписать их значения при
. Чтобы убедиться в этом, достаточно выписать их значения при ![]() . Действительно,
. Действительно, ![]() пробегает значения
пробегает значения 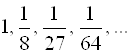 , а
, а 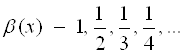 .
.
Cледовательно, надо как-то различать бесконечно малые по характеру их изменения.
Определение. Пусть ![]() и
и ![]() – бесконечно малые при
– бесконечно малые при ![]() и
и  . Если:
. Если:
1) ![]() , то
, то ![]() и
и ![]() называются бесконечно малыми одного порядка малости.
называются бесконечно малыми одного порядка малости.
2) ![]() , то
, то ![]() и
и ![]() называются эквивалентными бесконечно малыми, и пишут
называются эквивалентными бесконечно малыми, и пишут ![]() .
.
3) ![]() , то
, то ![]() называется бесконечно малой более высокого порядка малости, чем
называется бесконечно малой более высокого порядка малости, чем ![]() , и пишут
, и пишут ![]() .
.
4) ![]() , то
, то ![]() имеет более высокий порядок малости, чем
имеет более высокий порядок малости, чем ![]() .
.
Eсли 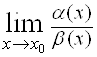 не существует, то
не существует, то ![]() и
и ![]() называются несравнимыми.
называются несравнимыми.
Сравним бесконечно малые ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() с бесконечно малой
с бесконечно малой ![]() при
при ![]() .
.
1)  ,
,  ,
,

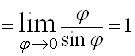 , следовательно при
, следовательно при ![]()
![]()
![]() .
.
2) ![]() , значит,
, значит, ![]() и
и ![]() при
при ![]() одного порядка малости.
одного порядка малости.
3)  , откуда следует, что
, откуда следует, что ![]() является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем ![]() .
.
4)  , значит,
, значит, ![]() есть бесконечно малая низшего порядка, чем
есть бесконечно малая низшего порядка, чем ![]() .
.
Величины 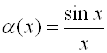 и
и  являются бесконечно малыми при
являются бесконечно малыми при ![]() и
и 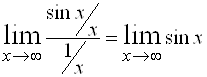 не существует, следовательно, эти величины несравнимые.
не существует, следовательно, эти величины несравнимые.
Часто оказывается недостаточно знать, что из двух бесконечно малых одна является более высокого порядка малости, чем другая, нужно еще как-то оценить насколько высок этот порядок.
Определение. Число ![]() называется порядком малости бесконечно малой
называется порядком малости бесконечно малой ![]() по отношению к бесконечно малой
по отношению к бесконечно малой ![]() , если
, если ![]() и
и ![]() являются бесконечно малыми одного порядка, то есть если
являются бесконечно малыми одного порядка, то есть если 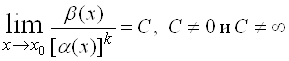 .
.
Пример 1. Определить порядок малости бесконечно малых ![]() ,
, ![]() и
и ![]() относительно
относительно ![]() при
при ![]() .
.
1) 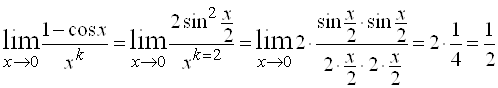 , то есть
, то есть ![]() является бесконечно малой второго порядка малости по отношению к
является бесконечно малой второго порядка малости по отношению к ![]() .
.
2) Бесконечно малые ![]() и
и ![]() одного порядка малости поскольку
одного порядка малости поскольку 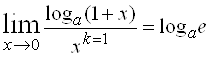 .
.
3) 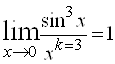 , т. е.
, т. е. ![]() имеет третий порядок малости относительно
имеет третий порядок малости относительно ![]() .
.
Обычно при сравнении бесконечно малых одну из них выбирают в качестве эталона и называют основной. Если бесконечно малые являются функциями от ![]() и становятся бесконечно малыми при
и становятся бесконечно малыми при ![]() , то за основную бесконечно малую принимают величину
, то за основную бесконечно малую принимают величину ![]() , если
, если ![]() – конечно и
– конечно и ![]() , если
, если ![]() .
.
Пусть ![]() – основная бесконечно малая, тогда бесконечно малую
– основная бесконечно малая, тогда бесконечно малую ![]() , где
, где ![]() – константы и
– константы и ![]() , считают простейшей бесконечно малой.
, считают простейшей бесконечно малой.
Определение. Простейшую бесконечно малую ![]() , эквивалентную данной бесконечно малой
, эквивалентную данной бесконечно малой ![]() , называют ее главной частью
, называют ее главной частью
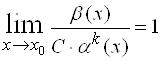 . (6)
. (6)
В частности, при ![]() главная часть имеет вид
главная часть имеет вид ![]() , а при
, а при ![]() –
– ![]() .
.
Пример 2. Выделить главную часть бесконечно малых ![]() ,
, ![]() и
и ![]() при
при ![]() . (Сравните с примером 1).
. (Сравните с примером 1).
Решение. Основной бесконечно малой будет ![]() , следовательно, вид главной части у всех
, следовательно, вид главной части у всех ![]() будет
будет ![]() .
.
1)  , если
, если ![]() и
и 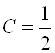 , тогда
, тогда  .
.
2) 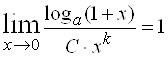 , при
, при ![]() и
и ![]() ,
, ![]() .
.
3)  , если
, если ![]() ,
, ![]() , главная часть
, главная часть ![]() .
.
Пример 3. Пусть ![]() . Выделить главную часть бесконечно малой
. Выделить главную часть бесконечно малой ![]() .
.
Решение. Основной бесконечно малой будет ![]() , тогда главную часть будем искать в виде
, тогда главную часть будем искать в виде ![]() . Найдем, при каких
. Найдем, при каких ![]() и
и ![]()
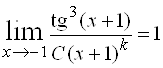 . Очевидно, что
. Очевидно, что  , отсюда следует, что главной частью будет
, отсюда следует, что главной частью будет ![]() .
.
Пример 4. Пусть ![]() . Выделить главную часть бесконечно малой
. Выделить главную часть бесконечно малой ![]() .
.
Решение. В данном случае ![]() и главная часть имеет вид
и главная часть имеет вид ![]() . Определим
. Определим ![]() и
и ![]() :
:
 .
.
Главная часть ![]() .
.
Пример 5. Выделить главную часть бесконечно малой  при
при ![]() .
.
Решение. Записываем основную бесконечно малую 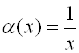 и вид главной части
и вид главной части  . Тогда
. Тогда
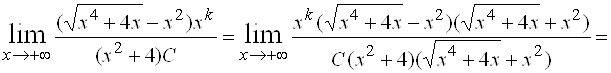
 .
.
Искомая главная часть ![]() .
.
Для данной бесконечно малой может существовать много эквивалентных бесконечно малых, но главная часть у нее одна. Например, при ![]()
![]() , но главная часть у всех одна и равна
, но главная часть у всех одна и равна ![]() (все остальные не являются простейшими).
(все остальные не являются простейшими).
При раскрытии неопределенности ![]() полезно пользоваться следующими теоремами:
полезно пользоваться следующими теоремами:
Теорема 1. Сумма конечного числа бесконечно малых при ![]() различных порядков малости эквивалентна слагаемому низшего порядка малости.
различных порядков малости эквивалентна слагаемому низшего порядка малости.
Сумма ![]() , если
, если  , то есть
, то есть ![]() – главная часть этой суммы.
– главная часть этой суммы.
Теорема 2. Предел отношения бесконечно малых не изменится при замене этих бесконечно малых им эквивалентными.
Пример 6. 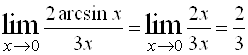 .
.
Пример 7. 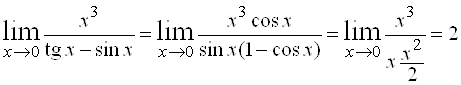 .
.
Замечания.
1. В теореме 2 говорится о возможности замены только всего выражения, стоящего в числителе или знаменателе.
2. В тех случаях, когда числитель или знаменатель представляет собой произведение бесконечно малых, то каждую из них можно заменить эквивалентной, так как и все произведение заменится эквивалентной величиной.
3. Если в числителе или знаменателе стоит сумма, то нельзя при раскрытии неопределенности заменять отдельные слагаемые эквивалентными величинами, поскольку такая замена может привести к неверному результату или вовсе к потере смысла.
4. При вычислении предела бесконечно малую можно заменять ее главной частью.
Сравнение бесконечно больших в точке ![]() функций и отыскание их главных частей производится аналогично.
функций и отыскание их главных частей производится аналогично.
Пример 8. При ![]() бесконечно большая
бесконечно большая ![]() низшего порядка роста по сравнению с бесконечно большой
низшего порядка роста по сравнению с бесконечно большой ![]() , так как
, так как
 .
.
Пример 9. Определить порядок роста бесконечно большой ![]() по отношению к бесконечно большой
по отношению к бесконечно большой ![]() при
при ![]() .
.
Решение. Решение сводится к отысканию такого числа ![]() , при котором
, при котором 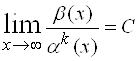 ,
, ![]() . Очевидно,
. Очевидно,

 . Итак,
. Итак, ![]() – бесконечно большая второго порядка по отношению к
– бесконечно большая второго порядка по отношению к ![]() .
.
Пример 10. Пусть ![]() . Выделить главную часть бесконечно большой
. Выделить главную часть бесконечно большой 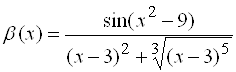 .
.
Решение. Из условия ![]() получаем, что
получаем, что ![]() – основная бесконечно малая, тогда
– основная бесконечно малая, тогда 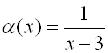 – основная (эталонная) бесконечно большая, следовательно, главная часть будет иметь вид
– основная (эталонная) бесконечно большая, следовательно, главная часть будет иметь вид 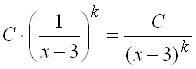 .
.
Находим 

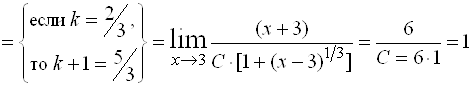 , то есть главная часть
, то есть главная часть 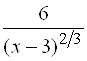 .
.
Для самостоятельной работы.
1. Определить порядок малости при ![]() относительно
относительно ![]() следующих функций:
следующих функций:
![]() ; Ответ: 1;
; Ответ: 1;
![]() ; Ответ: 2;
; Ответ: 2;
![]() ; Ответ: 4.
; Ответ: 4.
2. Пусть ![]() . Выделить главные части следующих функций:
. Выделить главные части следующих функций:
А) ![]() ; Ответ:
; Ответ: ![]() ;
;
Б) ![]() ; Ответ:
; Ответ: ![]() ;
;
В) ![]() ; Ответ:
; Ответ: 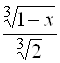 .
.
3. Определить порядок роста бесконечно больших величин и выделить их главные части:
А)  , при
, при ![]() ; Ответ:
; Ответ: 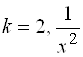 ;
;
Б) ![]() , при
, при ![]() ; Ответ:
; Ответ:  ;
;
В) 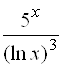 , при
, при ![]() ; Ответ:
; Ответ: 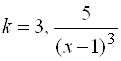 .
.
| < Предыдущая | Следующая > |
|---|