5.07.3 Примеры на вычисление пределов функций

Вычислить указанные пределы:

1. .

2.

.

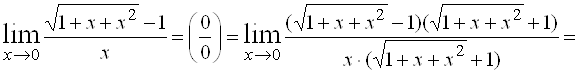
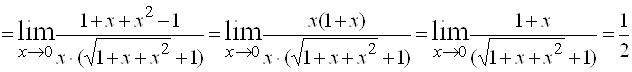3. 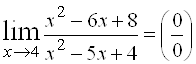. Так как числитель и знаменатель обратились в нуль при , то – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет . Получаем

.

4.

.

5.

.

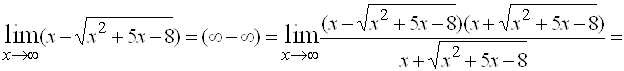
6. – не существует, так как .

7. . Обозначим , причем заметим, что при . Получим

.

8. . (Ответ получается непосредственно подстановкой вместо .)

9. . Здесь следует рассмотреть односторонние пределы:

; .

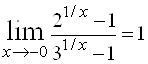Следовательно, 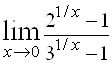– не существует (так как у функции разные односторонние пределы).

Для самостоятельного решения.

1) ; Ответ:.

2) ; Ответ: .

3) 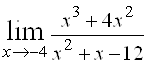; Ответ: .

4) 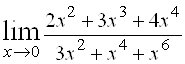; Ответ: .

5) . Ответ: не существует.

6) ; Ответ: .

7) 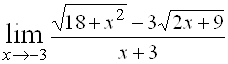; Ответ: .

8) Найти в точке односторонние пределы функции ; Ответ: .

9) 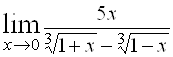; Ответ: .

< Предыдущая		Следующая >