5.07.2 Односторонние пределы и их связь с пределом

Когда мы формулировали определение предела функции в точке , то не делали никакого ограничения на способ стремления значений к , т. е. точка могла стремиться к точке и справа, и слева. Если в определении предела функции потребовать, чтобы стремилось к не любым способом, а только слева (оставаясь все время меньше ) или только справа (оставаясь больше ), то получим определение предела слева и справа в точке .

Определение. Число называется пределом функции при , стремящемся к слева, если для любого , найдется такое , что для всех , удовлетворяющих неравенству , выполняется неравенство .

Определение предела функции при , стремящемся к справа, формулируется аналогично, с той лишь разницей, что выполнение неравенства требуется для из правой полуокрестности : .

Пределы слева и справа иначе называются односторонними пределами и соответственно обозначаются так:

, .

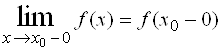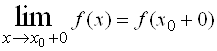Из определения предела следует, что если функция имеет в какой–либо внутренней точке промежутка предел, то она имеет в этой точке и односторонние пределы, причем

.

Но функция может иметь односторонние пределы и при отсутствии предела в точке, например, пусть

Таким образом , , следовательно в точке эта функция не имеет предела.

Если же функция в некоторой точке имеет односторонние пределы, причем , то их общее значение будет пределом функции в этой точке.

Все сформулированные выше теоремы о пределах и все изложенное в пункте 5.6 относительно неопределенностей легко переносятся на случай функций, если воспользоваться определением предела функции на языке последовательностей.

Понятия бесконечно малой и бесконечно большой переменной можно перенести на функцию.

Определение. Функция называется бесконечно малой при , если . Функция называется бесконечно большой при , если .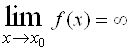

Например, функция является бесконечно малой при (так как 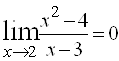) и бесконечно большой при (так как ).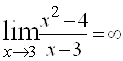

< Предыдущая		Следующая >