5.07.1 Понятие предела функции
Пусть функция ![]() определена на некотором промежутке
определена на некотором промежутке ![]() и
и ![]() – предельная точка для множества
– предельная точка для множества ![]() . Возьмем из
. Возьмем из ![]() последовательность точек, отличных от
последовательность точек, отличных от ![]() :
:
![]() (2)
(2)
Сходящуюся к ![]() . Значения функции в точках этой последовательности тоже образуют числовую последовательность
. Значения функции в точках этой последовательности тоже образуют числовую последовательность
![]() , (3)
, (3)
Которая может оказаться сходящейся или расходящейся. Поскольку выбор последовательности (2) ничем не обусловлен, кроме того только, чтобы она сходилась к точке ![]() , то ее можно составлять различными способами. Соответственно и последовательностей (3) можно составить сколько угодно. Если все последовательности (3) имеют своим пределом одно и то же число
, то ее можно составлять различными способами. Соответственно и последовательностей (3) можно составить сколько угодно. Если все последовательности (3) имеют своим пределом одно и то же число ![]() , то говорят, что функция
, то говорят, что функция ![]() имеет в точке
имеет в точке ![]() предел, равный
предел, равный ![]() .
.
Если же хотя бы одна из последовательностей (3) имеет предел, отличный от ![]() , или вообще не имеет предела, то говорят, что в точке
, или вообще не имеет предела, то говорят, что в точке ![]() функция
функция ![]() предела не имеет.
предела не имеет.
Дадим теперь строгое определение предела функции в точке «на языке последовательностей».
Определение. (По Гейне). Число ![]() называется пределом функции
называется пределом функции ![]() в точке
в точке ![]() , если для любой последовательности точек из области определения функции, отличных от
, если для любой последовательности точек из области определения функции, отличных от ![]() , сходящейся к точке
, сходящейся к точке ![]() (
(![]() ), последовательность соответствующих значений функции сходится к числу
), последовательность соответствующих значений функции сходится к числу ![]() .
.
Обозначают: ![]() , или
, или ![]() при
при ![]() .
.
Существует другое определение предела функции в точке, которое называют определением «на языке ![]() » или определением «на языке неравенств». Оно принадлежит Коши.
» или определением «на языке неравенств». Оно принадлежит Коши.
Определение. (По Коши). Число ![]() называется пределом
называется пределом ![]() в точке
в точке ![]() , если для любого
, если для любого ![]() , найдется такое число
, найдется такое число ![]() , что для всех
, что для всех ![]() ,
, ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , выполняется неравенство
, выполняется неравенство ![]() .
.
Определения по Коши и по Гейне эквивалентны (то есть одно следует из другого), поэтому можно пользоваться любым из них.
Пример 1. По определению предела доказать, что функция ![]() имеет в точке
имеет в точке ![]() предел, равный
предел, равный ![]() . Каково должно быть
. Каково должно быть ![]() , если
, если ![]() равно 1,
равно 1, ![]() и
и ![]() ?
?
Решение. Возьмем любое ![]() . Задача состоит в том, чтобы по этому
. Задача состоит в том, чтобы по этому ![]() найти такое
найти такое ![]() , при котором из неравенства
, при котором из неравенства ![]() следовало бы неравенство
следовало бы неравенство ![]() . Преобразуем последнее неравенство к виду
. Преобразуем последнее неравенство к виду ![]() или
или  . Отсюда видно, что можно взять
. Отсюда видно, что можно взять  . В частности, если
. В частности, если ![]() , то
, то 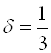 ; если
; если ![]() , то
, то ![]() ; если
; если  , то
, то 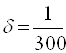 .
.
Пример 2. Пользуясь определением предела, показать, что ![]() .
.
Решение. Пусть ![]() произвольное положительное число. Найдем такое число
произвольное положительное число. Найдем такое число ![]() (разумеется оно будет зависеть от
(разумеется оно будет зависеть от ![]() ), чтобы для всех
), чтобы для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , выполнялось неравенство
, выполнялось неравенство ![]() . Преобразуем
. Преобразуем ![]() . Используя неравенство
. Используя неравенство ![]() , оценим
, оценим ![]() :
: ![]()
![]() . Следовательно,
. Следовательно, ![]() . Для выполнения неравенства
. Для выполнения неравенства ![]() достаточно потребовать, чтобы
достаточно потребовать, чтобы ![]() , то есть чтобы
, то есть чтобы ![]() . Отсюда
. Отсюда ![]() (второй корень уравнения равный
(второй корень уравнения равный ![]() отбрасываем, так как
отбрасываем, так как ![]() ).
).
Пример 3. Пользуясь определением предела функции в точке, доказать, что ![]() .
.
Решение. Воспользуемся определением предела функции «на языке последовательностей». Пусть ![]() – произвольная последовательность значений
– произвольная последовательность значений ![]() , сходящаяся к 2, то есть
, сходящаяся к 2, то есть ![]() . Тогда
. Тогда  и
и 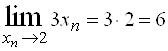 . По теореме о пределе суммы получим:
. По теореме о пределе суммы получим:
 .
.
Определение. (бесконечный предел). Говорят, что функция ![]() имеет в точке
имеет в точке ![]() бесконечный предел, если для любого
бесконечный предел, если для любого ![]() найдется такое число
найдется такое число ![]() , что для всех
, что для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , выполняется неравенство
, выполняется неравенство ![]() . Обозначается
. Обозначается 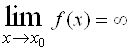 или
или ![]() при
при ![]() .
.
Аналогично определяются и соотношения 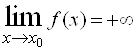 и
и  .
.
Определение. (предел функции на бесконечности). Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() , если для любого
, если для любого ![]() найдется такое вещественное число
найдется такое вещественное число ![]() , что
, что ![]() для всех
для всех ![]() .
.
Пример 4. Пользуясь определением предела функции на бесконечности, доказать, что ![]() .
.
Решение. Возьмем произвольное ![]() и определим значения
и определим значения ![]() , для которых выполняется неравенство
, для которых выполняется неравенство
![]() . (*)
. (*)
Так как ![]() при любом
при любом ![]() , то неравенство (*) можно переписать так:
, то неравенство (*) можно переписать так: ![]() , или
, или ![]() . Логарифмируя по основанию
. Логарифмируя по основанию ![]() , получим:
, получим: 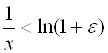 , откуда
, откуда 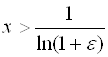 . Если за
. Если за ![]() взять число
взять число  , то для всех
, то для всех ![]() будет
будет ![]() , следовательно,
, следовательно, ![]() .
.
Предлагаем читателю самостоятельно сформулировать на языке неравенств определения пределов: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
| < Предыдущая | Следующая > |
|---|