5.05 Арифметические действия над переменными величинами

При практическом нахождении пределов применяются следующие теоремы о пределах.

Теорема 1. Если переменная имеет конечный предел, то она ограничена.

Теорема 2. Если переменная величина имеет предел, то он единственный.

Теорема 3. Предел постоянной равен самой постоянной (следует из определения предела).

Теорема 4. Если , , где и – конечны, то:

1) ;

2) ;

3) 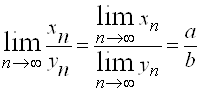, при условии, что .

В качестве следствия к пункту 2) отметим, что постоянный множитель можно выносить за знак предела, то есть .

Пример 1. Переменная имеет предел . Найти предел переменной .

Решение. По теореме 4 получим:

.

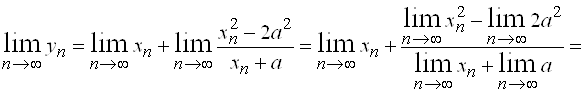
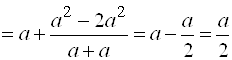Пример 2. Найти предел переменной .

Решение. .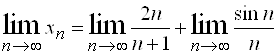

Поделив в первом слагаемом числитель и знаменатель на и применив теорему о пределе частного, получим: 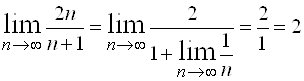(так как при ).

Второе слагаемое можно рассматривать как произведени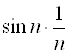е , где – величина ограниченная (так как ), а – бесконечно малая. Следовательно, – также величина бесконечно малая, то есть ее предел равен нулю. Таким образом, .

Обращаем внимание на то, что требование существования конечных пределов у переменных и в теореме 4 является существенным. Без этого условия теорема неверна, хотя предел суммы, разности, произведения и частного может существовать.

< Предыдущая		Следующая >