5.06 Особые случаи пределов и неопределенности
В пункте 5.5 указаны способы нахождения пределов суммы, разности, произведения и частного переменных ![]() и
и ![]() , имеющих конечные пределы. Рассмотрим теперь случаи, которые не охватываются указанными способами.
, имеющих конечные пределы. Рассмотрим теперь случаи, которые не охватываются указанными способами.
Начнем с частного 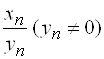 .
.
1) Пусть ![]() , тогда
, тогда  , так как
, так как  .
.
Здесь, и в дальнейшем, символом 0 обозначена бесконечно малая величина, символом ![]() – бесконечно большая величина,
– бесконечно большая величина, ![]() – величина, обратная бесконечно большой (см. теорему о связи между бесконечно малыми и бесконечно большими величинами).
– величина, обратная бесконечно большой (см. теорему о связи между бесконечно малыми и бесконечно большими величинами).
2) Если ![]() , то
, то  , так как
, так как 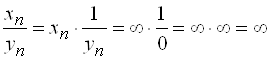 .
.
3) Пусть ![]() и
и ![]() , то есть
, то есть ![]() и
и ![]() – бесконечно малые величины. В этом случае о пределе отношения никакого общего заключения сделать нельзя, так как в зависимости от характера изменения
– бесконечно малые величины. В этом случае о пределе отношения никакого общего заключения сделать нельзя, так как в зависимости от характера изменения ![]() и
и ![]() возможны различные ответы. Так, например,
возможны различные ответы. Так, например,
А) если 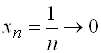 ,
, 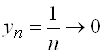 , то
, то 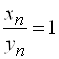 ;
;
Б) если 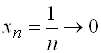 ,
, 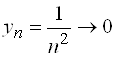 , то
, то 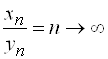 ;
;
В) если  ,
, 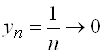 , то
, то  ;
;
Г) если 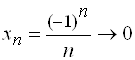 ,
, 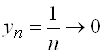 , то
, то  и предела не имеет.
и предела не имеет.
Таким образом, отношение бесконечно малых может быть величиной бесконечно малой, бесконечно большой, может иметь пределом число, отличное от нуля, а может и вовсе не иметь предела. В связи с этим говорят, что отношение бесконечно малых представляет собой Неопределенность и обозначают этот вид неопределенности символом ![]() . Когда предел отношения бесконечно малых найден или установлено, что его нет, то говорят, что неопределенность раскрыта.
. Когда предел отношения бесконечно малых найден или установлено, что его нет, то говорят, что неопределенность раскрыта.
Аналогично рассматривается случай, когда ![]() и говорят о неопределенности вида
и говорят о неопределенности вида ![]() .
.
В случае суммы ![]() результаты таковы:
результаты таковы:
1) если ![]() , то
, то ![]() ;
;
2) если ![]() , то
, то ![]() , то есть сумма бесконечно больших Одного знака, есть величина бесконечно большая;
, то есть сумма бесконечно больших Одного знака, есть величина бесконечно большая;
3) если ![]() и
и ![]() – бесконечно большие разных знаков, то
– бесконечно большие разных знаков, то ![]() в общем случае представляет собой неопределенность, которая обозначается символом
в общем случае представляет собой неопределенность, которая обозначается символом ![]() .
.
В случае произведения ![]() представляет интерес случай, когда один из сомножителей является бесконечно малой величиной, а другой – бесконечно большой. Пусть
представляет интерес случай, когда один из сомножителей является бесконечно малой величиной, а другой – бесконечно большой. Пусть ![]() , тогда
, тогда 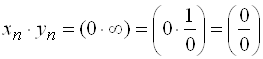 или
или 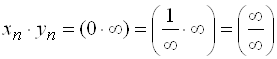 , а эти неопределенности уже рассмотрены.
, а эти неопределенности уже рассмотрены.
Кроме неопределенностей вида 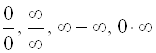 , существуют и другие неопределенности, с которыми познакомимся чуть позже.
, существуют и другие неопределенности, с которыми познакомимся чуть позже.
Рассмотрим на примерах наиболее типичные приемы раскрытия неопределенностей.
Пример 1. Найти  .
.
Решение. Числитель и знаменатель являются бесконечно большими, следовательно, имеем случай неопределенности вида ![]() . Для раскрытия неопределенности поделим числитель и знаменатель на
. Для раскрытия неопределенности поделим числитель и знаменатель на ![]() :
:
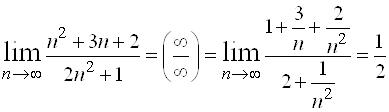 , так как
, так как 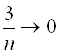 ,
, 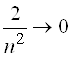 ,
,  при
при ![]() .
.
Пример 2. Найти  .
.
Решение. Данное выражение представляет собой неопределенность вида ![]() . Этот вид неопределенности раскрывается другим приемом. Умножим и разделим данное выражение на сумму
. Этот вид неопределенности раскрывается другим приемом. Умножим и разделим данное выражение на сумму ![]() , в результате придем к неопределенности вида
, в результате придем к неопределенности вида ![]() , которая раскрывается приемом, изложенным в примере 1.
, которая раскрывается приемом, изложенным в примере 1.

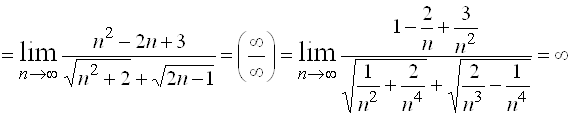 .
.
В этом примере мы использовали теорему о пределе корня: если ![]() , то
, то ![]() при любом натуральном
при любом натуральном ![]() .
.
Пример 3. Найти  .
.
Решение. 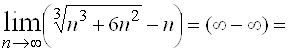

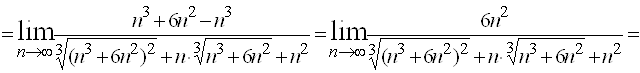

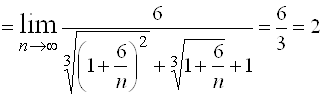 .
.
Пример 4. Найти  .
.
Решение. Так как 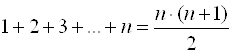 , то
, то
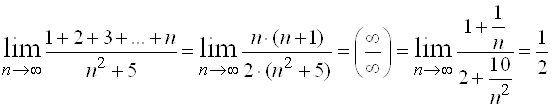 .
.
Пример 5. Найти 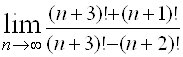 .
.
Решение. Напомним, что ![]() . Разделив числитель и знаменатель на
. Разделив числитель и знаменатель на ![]() , получим:
, получим:  .
.
Пример 6. Найти  .
.
Решение. В числителе и знаменателе находятся бесконечно убывающие геометрические прогрессии со знаменателями  и
и  соответственно, поэтому
соответственно, поэтому
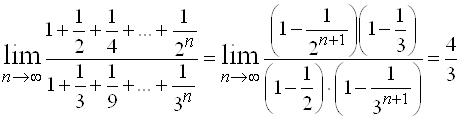 .
.
Пример 7. Найти  .
.
Решение. Так как
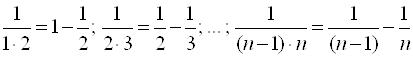 , то
, то
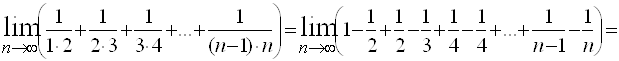
 .
.
Для самостоятельного решения.
Найти следующие пределы:
1.  ; Ответ:
; Ответ: ![]() .
.
2.  ; Ответ: 1.
; Ответ: 1.
3.  ; Ответ: 0.
; Ответ: 0.
4. 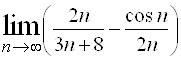 ; Ответ:
; Ответ: ![]() .
.
5. 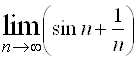 ; Ответ: не существует.
; Ответ: не существует.
6.  ; Ответ: 1.
; Ответ: 1.
7. 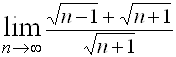 ; Ответ: 2.
; Ответ: 2.
8. 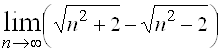 ; Ответ: 0.
; Ответ: 0.
9. 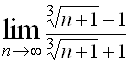 ; Ответ: 1.
; Ответ: 1.
10. 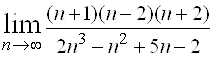 ; Ответ:
; Ответ: ![]() .
.
11. 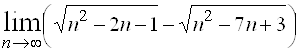 ; Ответ:
; Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|