5.04 Бесконечно малые и бесконечно большие величины

Определение. Переменная величина называется бесконечно малой при , если . Иначе: называется бесконечно малой, если для любого , найдется , что для всех выполняется неравенство .

Было бы ошибочно думать, что бесконечно малая величина может принимать только малые значения. Для нее характерным является не то, какие значения она принимает, а то, что ее пределом является число 0. Амплитуда затухающего колебания маятника – пример бесконечно малой величины.

Определение. Переменная называется бесконечно большой при , если для любого положительного числа , как бы велико оно ни было, найдется такое, что для всех .

О бесконечно большой переменной говорят, что она имеет бесконечный предел и пишут , однако это обозначение условно, так как знак равенства можно ставить между числами. Связь между бесконечно малой и бесконечно большой устанавливается следующей теоремой.

Теорема. Пусть (значения при любом ). Если – бесконечно малая при , то обратная ей величина – бесконечно большая при ; если – бесконечно большая, то – бесконечно малая при .

Иногда бесконечно малую величину будем условно обозначать символом 0, а бесконечно большую – символом .

Пример 1. Пользуясь определением бесконечно большой величины, доказать, что есть величина бесконечно большая.

Решение. Возьмем произвольное и решим неравенство , то есть . Логарифмируя, получим , откуда 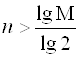. Если теперь взять , то для всех будет выполняться неравенство . Так как число можно взять сколь угодно большим, а значения превзойдут это число, то согласно определению переменная будет бесконечно большой.

Свойства бесконечно малых.

1) Сумма конечного числа бесконечно малых есть величина бесконечно малая.

2) Произведение ограниченной переменной на бесконечно малую есть величина бесконечно малая.

3) Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.

4) Произведение конечного числа бесконечно малых есть величина бесконечно малая.

5) Разность двух бесконечно малых есть величина бесконечно малая.

< Предыдущая		Следующая >