5.02 Сегмент, интервал, окрестность
Определение. Множество вещественных чисел ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , называется сегментом или отрезком (обозначается
, называется сегментом или отрезком (обозначается ![]() ), а удовлетворяющих строгому неравенству
), а удовлетворяющих строгому неравенству ![]() – интервалом (обозначается
– интервалом (обозначается ![]() ). Числа
). Числа ![]() и
и ![]() называются концами, а число
называются концами, а число ![]() – длиной как сегмента
– длиной как сегмента ![]() , так и интервала
, так и интервала ![]() .
.
Определение. Множество вещественных чисел ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() или
или ![]() , называется полусегментом или полуинтервалом и обозначается соответственно
, называется полусегментом или полуинтервалом и обозначается соответственно ![]() или
или ![]() .
.
Интервалы и полуинтервалы могут быть и бесконечными. Для обозначения множества вещественных чисел пользуются символом ![]() . Знаки
. Знаки ![]() и
и ![]() не являются числами, (а являются только символами) и для них нельзя указать соответствующих точек прямой. Поэтому в обозначениях интервалов со стороны таких знаков квадратные скобки не ставят. Сегменты, интервалы и полуинтервалы (конечные и бесконечные) объединяют под общим названием – промежутки.
не являются числами, (а являются только символами) и для них нельзя указать соответствующих точек прямой. Поэтому в обозначениях интервалов со стороны таких знаков квадратные скобки не ставят. Сегменты, интервалы и полуинтервалы (конечные и бесконечные) объединяют под общим названием – промежутки.
Определение. Окрестностью точки ![]() называется любой интервал, содержащий эту точку.
называется любой интервал, содержащий эту точку.
Часто рассматривают симметричную окрестность точки ![]() , то есть интервал
, то есть интервал ![]() , при этом
, при этом ![]() называют радиусом окрестности.
называют радиусом окрестности.
Изобразим на прямой окрестность точки 5 радиуса 3:
![]() Для того, чтобы показать, что точка
Для того, чтобы показать, что точка ![]() находится в этой окрестности, воспользуемся неравенством
находится в этой окрестности, воспользуемся неравенством ![]() . В общем случае
. В общем случае ![]() – окрестность
– окрестность ![]() точки
точки ![]() может быть задана неравенством
может быть задана неравенством ![]() .
.
Определение. Окрестностью бесконечно удаленной точки называется внешность некоторого отрезка. Симметричной окрестностью точки ![]() называется внешность любого отрезка, симметричного относительно нуля.
называется внешность любого отрезка, симметричного относительно нуля.
С помощью неравенств ![]() – окрестность бесконечно удаленной точки записывается в виде
– окрестность бесконечно удаленной точки записывается в виде ![]() ,
, ![]() или, объединяя в одно неравенство,
или, объединяя в одно неравенство, ![]() .
.
Определение. Точка ![]() называется предельной точкой множества, если в любой ее окрестности содержится, по крайней мере, одна точка данного множества, отличная от
называется предельной точкой множества, если в любой ее окрестности содержится, по крайней мере, одна точка данного множества, отличная от ![]() .
.
Из определения следует, что в любой окрестности предельной точки содержится бесконечное число точек данного множества. Предельная точка множества может как принадлежать, так и не принадлежать самому множеству.
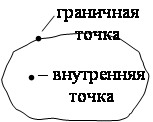 Определение. Точка
Определение. Точка ![]() называется внутренней точкой множества, если она принадлежит этому множеству вместе со своей окрестностью.
называется внутренней точкой множества, если она принадлежит этому множеству вместе со своей окрестностью.
Определение. Точка ![]() называется граничной точкой множества, если в любой ее окрестности есть точки как принадлежащие множеству, так и не принадлежащие ему. Сама граничная точка может как принадлежать множеству, так и не принадлежать ему.
называется граничной точкой множества, если в любой ее окрестности есть точки как принадлежащие множеству, так и не принадлежащие ему. Сама граничная точка может как принадлежать множеству, так и не принадлежать ему.
Совокупность граничных точек множества называется его границей.
Определение. Множество, содержащее все свои граничные точки, называется замкнутым, в противном случае – открытым.
Примеры: 1) для множества рациональных чисел ![]() граничными являются все точки отрезка
граничными являются все точки отрезка ![]() как рациональные, так и иррациональные;
как рациональные, так и иррациональные;
2) для множества точек  граничными являются сами точки этого множества и нуль.
граничными являются сами точки этого множества и нуль.
5.03 Числовая последовательность и ее предел
Если каждому натуральному числу ![]() сопоставить вещественное число
сопоставить вещественное число ![]() , тем самым зададим некоторые вещественные числа, определенным образом перенумерованные:
, тем самым зададим некоторые вещественные числа, определенным образом перенумерованные: ![]() имеет номер 1,
имеет номер 1, ![]() – номер 2 и т. д. Тогда говорят, что задана последовательность чисел, или числовая последовательность:
– номер 2 и т. д. Тогда говорят, что задана последовательность чисел, или числовая последовательность:
![]() , (1)
, (1)
Которая кратко обозначается ![]() .
.
Числа, составляющие последовательность, называются ее членами, а ![]() – общим или
– общим или ![]() -м членом последовательности. В отличие от числового множества, у которого все элементы различны, последовательность может иметь среди своих членов одинаковые, например:
-м членом последовательности. В отличие от числового множества, у которого все элементы различны, последовательность может иметь среди своих членов одинаковые, например: ![]() или
или ![]() Числовое значение
Числовое значение ![]() зависит от
зависит от ![]() , то есть является функцией от
, то есть является функцией от ![]() , поэтому числовая последовательность может рассматриваться как функция натурального аргумента.
, поэтому числовая последовательность может рассматриваться как функция натурального аргумента.
Пример 1. Последовательность задана общим членом  . Написать
. Написать ![]() члены последовательности.
члены последовательности.
Решение.  ,
,  ,
, 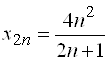 ,
, 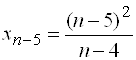 .
.
Для сокращения записей в дальнейшем будем использовать логические символы: квантор общности ![]() и квантор существования
и квантор существования ![]() . Запись
. Запись ![]() означает: любой (всякий)
означает: любой (всякий) ![]() , а
, а ![]() – существует (найдется)
– существует (найдется) ![]() .
.
Определение. Последовательность (1) называется ограниченной, если ![]() , такое, что
, такое, что ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Пример 2. Доказать, что последовательности 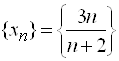 и
и  – ограниченные, а последовательность
– ограниченные, а последовательность  - не ограничена.
- не ограничена.
Решение. Очевидно, что для любого ![]() справедливо неравенство
справедливо неравенство  . Умножая на 3, получим
. Умножая на 3, получим  .
.
Оценим по модулю общий член последовательности ![]() :
: 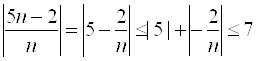 .
.
Предположим, что последовательность ![]() ограничена сверху, то есть существует число
ограничена сверху, то есть существует число ![]() такое, что
такое, что  , тогда
, тогда ![]() или
или ![]() , т. е. неравенство
, т. е. неравенство ![]() выполняется не для всех
выполняется не для всех ![]() , а только для
, а только для ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() , следовательно,
, следовательно, ![]() не ограничена.
не ограничена.
Определение. Число ![]() называется пределом числовой последовательности
называется пределом числовой последовательности ![]() при
при ![]() , если для всякого
, если для всякого ![]() можно указать номер
можно указать номер ![]() , такой, что для всех членов последовательности с номерами
, такой, что для всех членов последовательности с номерами ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Обозначают ![]() или
или ![]() и говорят, что последовательность сходится к
и говорят, что последовательность сходится к ![]() . Если последовательность не имеет конечного предела, то ее называют расходящейся. Заметим, что величина
. Если последовательность не имеет конечного предела, то ее называют расходящейся. Заметим, что величина ![]() зависит от
зависит от ![]() , которое выбирается произвольно. Чем меньше
, которое выбирается произвольно. Чем меньше ![]() , тем
, тем ![]() , вообще говоря, будет больше (за исключением случая, когда последовательность состоит из одинаковых членов). Очевидно, что если
, вообще говоря, будет больше (за исключением случая, когда последовательность состоит из одинаковых членов). Очевидно, что если ![]() и неравенство
и неравенство ![]() выполняется при
выполняется при ![]() , то оно подавно будет выполняться при
, то оно подавно будет выполняться при ![]() .
.
Пример 3. Показать, что последовательность  имеет своим пределом число 1.
имеет своим пределом число 1.
Решение. По определению предела числовой последовательности ![]()
![]() ,
, ![]()
 .
.
Будем решать последнее неравенство относительно ![]() :
: 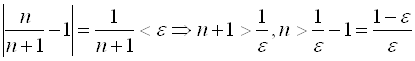 . Таким образом, получили, что неравенство
. Таким образом, получили, что неравенство  выполняется не для всех номеров
выполняется не для всех номеров ![]() , а только для тех, которые больше
, а только для тех, которые больше ![]() , следовательно, за
, следовательно, за ![]() можно взять целую часть числа
можно взять целую часть числа ![]() , то есть
, то есть 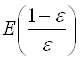 . Если окажется, что
. Если окажется, что 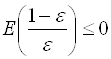 , то
, то ![]() можно взять равным 1. В определении говорится, что
можно взять равным 1. В определении говорится, что ![]() может быть любым положительным числом, в частности, если
может быть любым положительным числом, в частности, если ![]() , то
, то  , если
, если 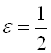 , то
, то  и т. д.
и т. д.
Пример 4. Показать, что последовательность, заданная общим числом  , имеет своим пределом число
, имеет своим пределом число ![]() .
.
Решение. Возьмем любое ![]() . Так как
. Так как 
 , то из неравенства
, то из неравенства 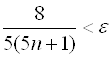 получим
получим  , то есть достаточно взять
, то есть достаточно взять  и тогда
и тогда  при
при ![]() .
.
Пример 5. Показать, что числовая последовательность с общим членом ![]() не имеет предела.
не имеет предела.
Решение. В подробной записи эта последовательность имеет вид: ![]()
Будем рассуждать от противного. Пусть последовательность имеет своим пределом некоторое число ![]() . Тогда по определению предела для любого
. Тогда по определению предела для любого ![]() , в том числе и для
, в том числе и для ![]() , найдется
, найдется ![]() , что
, что  для
для ![]() . Так как
. Так как ![]() принимает попеременно значения 1 и –1, то должно быть
принимает попеременно значения 1 и –1, то должно быть 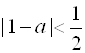 и
и  . Тогда получим
. Тогда получим  , то есть
, то есть ![]() , чего быть не может.
, чего быть не может.
Для доказательства того, что некоторое число ![]() не является пределом последовательности, достаточно убедиться, что не все требования, сформулированные в определении предела, выполнены. Допустим, что
не является пределом последовательности, достаточно убедиться, что не все требования, сформулированные в определении предела, выполнены. Допустим, что ![]() не является пределом данной последовательности. Это значит, что Нельзя для Любого
не является пределом данной последовательности. Это значит, что Нельзя для Любого ![]() найти соответствующий
найти соответствующий ![]() , о котором говорится в определении, то есть существует хотя бы одно
, о котором говорится в определении, то есть существует хотя бы одно ![]() , для которого невозможно найти такого
, для которого невозможно найти такого ![]() , чтобы неравенство
, чтобы неравенство ![]() выполнялось бы для всех
выполнялось бы для всех ![]() . Иначе говоря, найдется хотя бы одно значение
. Иначе говоря, найдется хотя бы одно значение ![]() , для которого
, для которого ![]() .
.
Пример 6. Доказать, пользуясь определением предела, что число ![]() не является пределом последовательности с общим членом
не является пределом последовательности с общим членом  .
.
Решение. Оценим снизу абсолютную величину разности ![]() :
: 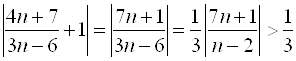 , так как
, так как  при любом
при любом ![]() . Следовательно, если взять в качестве
. Следовательно, если взять в качестве  , то
, то  и искать
и искать ![]() в соответствии с определением бессмысленно.
в соответствии с определением бессмысленно.
Дадим геометрическое истолкование предела числовой последовательности.
 |
Числовую последовательность можно рассматривать как последовательность точек прямой и о пределе можно говорить как о точке на прямой. Так как неравенство
![]()
![]() Вне этой окрестности может оказаться лишь Конечное число точек
Вне этой окрестности может оказаться лишь Конечное число точек ![]() .
.
Общий член последовательности можно рассматривать как переменную, принимающую эту последовательность значений, поэтому предел последовательности (1) называют также и пределом переменной ![]() .
.
Вопросы для самопроверки и упражнения.
1. Дана последовательность точек ![]()
![]() Все точки этой последовательности, начиная с пятой, находятся в окрестности нуля
Все точки этой последовательности, начиная с пятой, находятся в окрестности нуля ![]() . Почему из этого, однако, не следует, что точка нуль является пределом данной последовательности?
. Почему из этого, однако, не следует, что точка нуль является пределом данной последовательности?
2. Пользуясь определением предела числовой последовательности, доказать, что  . Начиная с какого
. Начиная с какого ![]() , будет
, будет ![]()
 ?
?
3. Доказать, что число 1 не является пределом переменной  .
.
4. Привести пример ограниченной последовательности, не имеющей предела.
| < Предыдущая | Следующая > |
|---|