5.01 О границах числовых множеств

Множество, элементами которого являются вещественные числа, будем называть числовым. Если множество состоит из конечного числа элементов, то его называют конечным, в противном случае – бесконечным.

Определение. Числовое множество называется ограниченным сверху, если существует такое вещественное число , что для любого элемента из множества выполняется неравенство . Число называется верхней границей .

Определение. Если существует такое число , что все элементы множества удовлетворяют неравенству , то множество называется ограниченным снизу, а число – его нижней границей.

Определение. Числовое множество называется ограниченным, если оно ограничено сверху и снизу, т. е. если для всех выполняется неравенство .

Если – верхняя, а – нижняя границы множества , то числа и тоже будут соответственно верхней и нижней границами этого множества. Следовательно, всякое ограниченное множество имеет бесконечно много верхних и нижних границ.

Определение. Наименьшая из всех верхних границ множества называется точной верхней границей этого множества (обозначается ). Наибольшая из всех нижних границ называется точной нижней границей этого множества (обозначается ).

Точная верхняя и точная нижняя границы могут как принадлежать данному множеству, так и не принадлежать ему.

Если не ограничено сверху, то пишут , если снизу, то .

На вопрос о том, всегда ли у ограниченного множества существуют точные границы, отвечает следующая теорема.

Теорема. Всякое непустое ограниченное сверху множество имеет точную верхнюю границу, а всякое непустое ограниченное снизу множество имеет точную нижнюю границу.

Пример 1. Даны множества , 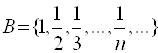и . Указать их точные границы.

Решение. – бесконечное, ограниченное снизу множество. Числа – его нижние границы, а . Сверху это множество не ограничено, т. е. . Множество – бесконечное ограниченное множество, т. е. оно ограничено и сверху, и снизу, его точные границы: , , – бесконечное множество, не ограниченное как сверху, так и снизу.

Любое конечное множество ограничено, так как среди его элементов всегда найдутся наибольшее и наименьшее числа, которые и будут точными границами. Обратное утверждение неверно, т. е. из ограниченности множества не следует его конечность, как это видно на примере множества .

Пример 2. Числовое множество состоит из всех чисел, для которых . Какие числа будут его границами?

Решение. Неравенство равносильно двойному неравенству , откуда видно, что число 3 и всякое большее число будет верхней границей, а число –3 и всякое меньшее число – его нижней границей. , .

Пример 3. Числовое множество состоит из чисел, удовлетворяющих условию . Укажите наименьшее число , удовлетворяющее неравенству для всех из данного множества. Какими границами для этого множества будут числа и ?

Решение. Так как равносильно неравенству , то за нужно взять такое положительное число, чтобы неравенства: и выполнялись одновременно. Это, очевидно, будет при , равном наибольшей из абсолютных величин чисел и , то есть при , при этом , a – верхняя (не точная) граница , точной верхней границей является .

Вопросы для самопроверки.

1. Приведите примеры ограниченных бесконечных множеств. Существуют ли конечные неограниченные множества?

2. Приведите примеры множеств, которым принадлежат их точные границы и множеств, которым не принадлежат их точные границы.

3. Приведите пример множества, которому принадлежит его точная нижняя граница, а точная верхняя не принадлежит.

< Предыдущая		Следующая >